What is the formula for finding the surface area of an inclined cone?

[Aphex_Twin]

The area (not including the base) of a right cone is pi*radius*sqrt(height^2+radius^2).

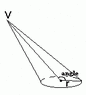
What is the area of an inclined cone? (Where the segment joining the tip and the center of the base circle is not perpendicular to the base plane).

So what is the area of this, considering we know the radius, height and inclination?

 

[mathwonk]

well if you open up a right cone, you just get a circle with a notch out of it, and that is how you compute the area. so your examp[les aeems to yield an ellipse with a notch out of it, but the notch does not cut to the center nor any simple spot inside the elipse. so i do noit see immediately how to do it unless i have a parametrization of the ellipse.

 

[AKG]

The surface area you desire will be the average of the surface areas for two right cones, one having a slant height equal to the shortest distance from the apex to the base (along the surface) and the other having a slant height equal to the greatest distance from the apex to the base (along the surface).

 

[arildno]

Let your base be in the xy-plane with centre at the origin, and let the coordinates of your apex be:
(a_{x},a_{y},a_{z})
Then, the surface of the cone is parametrized by:
\vec{S}(z,\theta)=R(1-\frac{z}{a_{z}})((\cos\theta-\frac{a_{x}}{R})\vec{i}+(\sin\theta-\frac{a_{y}}{R})\vec{j})+(a_{x}\vec{i}+a_{y}\vec{j}+z\vec{k}), 0\leq\theta\leq2\pi,0\leq{z}\leq{a}_{z}

Hence, the tangent vectors are:
\frac{\partial\vec{S}}{\partial\theta}=R(1-\frac{z}{a_{z}})(-\sin\theta\vec{i}+\cos\theta\vec{j})
\frac{\partial\vec{S}}{\partial{z}}=-\frac{R}{a_{z}}((\cos\theta-\frac{a_{x}}{R})\vec{i}+(\sin\theta-\frac{a_{y}}{R})\vec{j})+\vec{k}
The area is then given by:
A=\int_{0}^{2\pi}\int_{0}^{a_{z}}||\frac{\partial\vec{S}}{\partial\theta}\times\frac{\partial\vec{S}}{\partial{z}}||dzd\theta