What is the maximum of the given function in the closed square $D$?

Click For Summary

Discussion Overview

The discussion revolves around finding the maximum value of the function \( f(x_1,x_2) = x_1 + x_2 \) within the closed square \( D \) defined by the vertices \( (0,0), (1,0), (1,1), (0,1) \). Participants explore the conditions under which this maximum is achieved, considering aspects of linear programming and the evaluation of function values at specific points within the domain.

Discussion Character

  • Exploratory
  • Technical explanation
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • Some participants assert that the maximum value of \( f \) is \( 2 \) at the point \( (1,1) \), while others suggest it may be "an" optimal solution rather than "the" optimal solution.
  • There is a discussion about whether all other values of \( f \) within the square are smaller than \( 2 \), with some participants agreeing that this supports the claim of \( (1,1) \) being the maximum.
  • Participants mention the need to evaluate the function at the corner points of the square and consider the implications of including or excluding the boundary in determining the maximum.
  • One participant raises a question about the necessity of checking values at points like \( f\left( \frac{1}{m}, \frac{1}{n}\right) \) for natural numbers \( n \) and \( m \), prompting a discussion on the relevance of corner points in linear programming.
  • There is mention of taking partial derivatives and inspecting boundaries in general optimization problems, although it is noted that for linear programming, checking corner points suffices.

Areas of Agreement / Disagreement

Participants express differing views on whether \( (1,1) \) is definitively "the" maximum or merely "an" optimal solution. While there is agreement that the maximum value is \( 2 \), the discussion remains unresolved regarding the uniqueness of the optimal solution.

Contextual Notes

Participants highlight that the evaluation of the maximum relies on the properties of linear functions and the specific constraints of the problem, noting that the inclusion of boundaries is significant in determining the maximum value.

Who May Find This Useful

This discussion may be useful for individuals interested in optimization problems, linear programming, and mathematical reasoning related to function evaluation within defined domains.

evinda
Gold Member
MHB
Messages
3,741
Reaction score
0
Hello! (Wave)

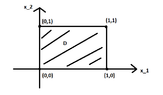
We consider the function $f(x_1,x_2)=x_1+x_2$ and the (closed) square $D$ with edges $(0,0), (1,0), (1,1), (0,1)$.

Check if $f$ has a maximum in $D$ and if so, find the points of $D$ at which this maximum is achieved.$$\max_{(x_1,x_2) \in D} (x_1+x_2)$$

View attachment 4792

$$(S)\left\{\begin{matrix}
x_1 \geq 0\\
x_2 \geq 0\\
x_1 \leq 1\\
x_2 \leq 1
\end{matrix}\right.$$

so $D=\{ (x_1, x_2) \in \mathbb{R}^2: x_1, x_2 \text{ satisfy } (S)\}$.

$$x_1, x_2 \geq 0$$

Obviously $\max_{(x_1, x_2) \in D} (x_1+x_2) \leq \max_{(x_1, x_2) \in D} x_1 + \max_{(x_1, x_2) \in D} x_2 \leq 1+1=2 $

and $\max_{(x_1, x_2) \in D} (x_1+x_2)=f(1,1)$, so $(1,1)$ is the optimal solution of the linear programming problem.
How do we deduce that the maximum of the given function is $2$. Because of the fact that the maximum is less or equal to $2$ and there is a point $(1,1)$ for which the value $2$ is achieved?
 

Attachments

  • square.png
    square.png
    2.8 KB · Views: 123
Physics news on Phys.org
evinda said:
Hello! (Wave)

and $\max_{(x_1, x_2) \in D} (x_1+x_2)=f(1,1)$, so $(1,1)$ is the optimal solution of the linear programming problem.

Small correction: it's "an" optimal solution.
We don't know yet if it is "the" optimal solution. (Nerd)
How do we deduce that the maximum of the given function is $2$. Because of the fact that the maximum is less or equal to $2$ and there is a point $(1,1)$ for which the value $2$ is achieved?

Yes. (Smile)

Still, I believe the question asks for "all" points... (Sweating)
 
I like Serena said:
Small correction: it's "an" optimal solution.
We don't know yet if it is "the" optimal solution. (Nerd)

Why? Aren't all the other values that $f$ could get smaller? Or am I wrong? (Thinking)
I like Serena said:
Yes. (Smile)

Still, I believe the question asks for "all" points... (Sweating)

So in order to show that we have one optimal solution do we have to reject the other feasible solutions?
 
evinda said:
Why? Aren't all the other values that $f$ could get smaller? Or am I wrong? (Thinking)

So in order to show that we have one optimal solution do we have to reject the other feasible solutions?

Indeed. And that's exactly the point.
Because all other values that $f$ could get are smaller, it is "the" maximum. (Happy)

Moveover, if the boundary were not included, there would be no maximum, only a supremum. (Nerd)
 
I like Serena said:
Indeed. And that's exactly the point.
Because all other values that $f$ could get are smaller, it is "the" maximum. (Happy)

Moveover, if the boundary were not included, there would be no maximum, only a supremum. (Nerd)

In order to reject the other feasible solutions do we have to compute the values $f(0,0), f(1,0), f(0,1)$ and the value of $f\left( \frac{1}{m}, \frac{1}{n}\right), n,m \in \mathbb{N}$ ? (Thinking)
 
evinda said:
In order to reject the other feasible solutions do we have to compute the values $f(0,0), f(1,0), f(0,1)$ and the value of $f\left( \frac{1}{m}, \frac{1}{n}\right), n,m \in \mathbb{N}$ ? (Thinking)

From a linear programming point of view, indeed we need to check all the corner points.
But that only works if the function to maximize is a linear function.

Where do your $f\left( \frac{1}{m}, \frac{1}{n}\right)$ come from? (Wondering)

More generally, we would take the partial derivatives and see where they are zero.
Additionally, we would inspect the boundaries to see if there is a maximum there.
For linear programming problems that can be simplified to just looking at the corner points. (Nerd)
 
I like Serena said:
From a linear programming point of view, indeed we need to check all the corner points.
But that only works if the function to maximize is a linear function.

Where do your $f\left( \frac{1}{m}, \frac{1}{n}\right)$ come from? (Wondering)

More generally, we would take the partial derivatives and see where they are zero.
Additionally, we would inspect the boundaries to see if there is a maximum there.
For linear programming problems that can be simplified to just looking at the corner points. (Nerd)

Ah I didn't know that if we have a linear programming problem we look only at the corner points. (Whew)

So we say that $\max_{(x_1, x_2) \in D} (x_1+x_2) \leq 2$ and

$$f(0,0)=0 \\ f(1,0)=1 \\ f(1,1)=2 \\ f(0,1)=1$$

thus the maximum of the function $f$ is $2$ and is achieved for $(x_1, x_2)=(1,1)$, right?
 
evinda said:
Ah I didn't know that if we have a linear programming problem we look only at the corner points. (Whew)

So we say that $\max_{(x_1, x_2) \in D} (x_1+x_2) \leq 2$ and

$$f(0,0)=0 \\ f(1,0)=1 \\ f(1,1)=2 \\ f(0,1)=1$$

thus the maximum of the function $f$ is $2$ and is achieved for $(x_1, x_2)=(1,1)$, right?

Yep! (Happy)
 
I like Serena said:
Yep! (Happy)

Nice... Thank you! (Smile)
 

Similar threads

Undergrad On inverse function theorem in Spivak's CoM
  • · Replies 6 ·
Replies
6
Views
3K
Undergrad Lipschitz continuity of vector-valued function
  • · Replies 3 ·
Replies
3
Views
3K
MHB Give a linear map that satisfies given properties
  • · Replies 3 ·
Replies
3
Views
2K
MHB Are the critical points minima or maxima?
  • · Replies 4 ·
Replies
4
Views
2K
MHB Finding Extrema under Constraints
  • · Replies 4 ·
Replies
4
Views
2K
MHB Extrema of function - What is λ?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Minimum of function under constraint
  • · Replies 10 ·
Replies
10
Views
3K
High School Is this a valid proof for the Extreme Value Theorem?
  • · Replies 14 ·
Replies
14
Views
2K
High School General explicit solution to polynomial interpolation
  • · Replies 3 ·
Replies
3
Views
2K
High School Are continuous functions on sequentially compact sets u-continuous?
  • · Replies 18 ·
Replies
18
Views
3K