Note that if we are to graph of $y=|x-1|+|2x-1|+|3x-1|+\cdots+|nx-1|$, we need to first determine the function for each piece from different interval, and each part in its interval is necessarily piecewise linear and hence the graph of $y$ will always looks like "elbow(\/)".
Therefore the minimum of $y=|x-1|+|2x-1|+|3x-1|+\cdots+|nx-1|$ occurs at $kx-1=0$ by the time we see the changes of the gradient of the linear function turns from negative to positive.
I will illustrate this with an example.
If we have $y=|x-1|+|2x-1|+|3x-1|+|4x-1|$ and we plot its graph, we see that we need to break the absolute function into 5 intervals:
[TABLE="class: grid, width: 820"]
[TR]
[TD]For $x>1$:
$y=x-1+2x-1+3x-1+4x-1=10x-4$[/TD]
[TD][/TD]
[/TR]
[TR]
[TD]For $\dfrac{1}{2}<x<1$:
$\begin{align*}y&=-(x-1)+2x-1+3x-1+4x-1\\&=-x+2x+3x+4x+1-1-1-1\\&=8x-2\end{align*}$[/TD]
[TD]For $\dfrac{1}{3}<x<\dfrac{1}{2}$:
$\begin{align*}y&=-(x-1)-(2x-1)+3x-1+4x-1\\&=-x-2x+3x+4x+1+1-1-1\\&=4x\end{align*}$[/TD]
[/TR]
[TR]
[TD]For $\dfrac{1}{4}<x<\dfrac{1}{3}$:
$\begin{align*}y&=-(x-1)-(2x-1)-(3x-1)+4x-1\\&=-x-2x-3x+4x+1+1+1-1\\&=-2x+2\end{align*}$[/TD]
[TD]For $x<\dfrac{1}{4}$:
$\begin{align*}y&=-(x-1)-(2x-1)-(3x-1)-(4x-1)\\&=-x-2x-3x-4x+1+1+1+1\\&=-10x+4\end{align*}$[/TD]
[/TR]
[/TABLE]
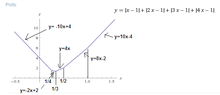
View attachment 4309From the graph, we can see that minimum of $y$ occurs at $3x-1=0$, i.e. $x=\dfrac{1}{3}$. This happens when the gradient of the piecewise linear function changes from $4$ ($y=4x$) to $-2$ ($y=-2x+2$). We can evaluate the minimum value by evaluating the function $-x-2x-3x+4x+1+1+1-1=-2x+2$ at $x=\dfrac{1}{3}$.
Now, back to the original problem to find the minimum of $y=|x-1|+|2x-1|+|3x-1|+\cdots+|nx-1|$. I know I need to focus on finding which $k$ value (from $kx-1$) does the gradient of the piecewise function changes from negative to positive. Since the only thing that matters is the gradient of the linear function, I will consider only all the coefficients of $x$ terms and discard the constants in finding for $k$. Here, $k$ is natural number.
$(1,\,2,\,3,\,\cdots,\,k-1),\,\,(k,\,k+1,\,\cdots,\,n)$
I know I need the sum from $(1,\,2,\,3,\,\cdots,\,k-1)$ is less than the sum from $(k,\,k+1,\,\cdots,\,n)$.
Therefore I get
$k\left(\dfrac{k-1}{2}\right)<(n+k)\left(\dfrac{n+1-k}{2}\right)$
I then solve the inequality above for natural number $k$, and obtain
$2k^2-2k-(n^2+n)<0$
$k=\left\lfloor\dfrac{1}{2}+\sqrt{\dfrac{1}{4}+\dfrac{n^2+n}{2}}\right\rfloor$
Now, to find for its minimum value, we subtract the sum of $kx-1+(k+1)x-1+\cdots+nx-1$ from the sum of $x-1+2x-1+\cdots+(k-1)x-1$ and remember to replace $x=\dfrac{1}{k}$ and get:
$\begin{align*}y_{\text{min}}&=(kx-1+nx-1)\left(\dfrac{n+1-k}{2}\right)-(x-1+(k-1)x-1)\left(\dfrac{k-1}{2}\right)\\&=(kx+nx-2)\left(\dfrac{n+1-k}{2}\right)-(kx-2)\left(\dfrac{k-1}{2}\right)\\&=\left(\dfrac{n}{k}-1\right)\left(\dfrac{n+1-k}{2}\right)+\left(\dfrac{k-1}{2}\right)\end{align*}$
where $k=\left\lfloor\dfrac{1}{2}+\sqrt{\dfrac{1}{4}+\dfrac{n^2+n}{2}}\right\rfloor$.