karush
Gold Member
MHB
- 3,240
- 5
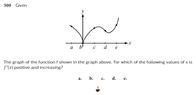
View attachment 9411image due to macros in overleaf
well apparently all we can do is solve this by observation
which would be the slope as x moves in the positive direction
e appears to be the only interval where the slope is always increasing
well apparently all we can do is solve this by observation
which would be the slope as x moves in the positive direction
e appears to be the only interval where the slope is always increasing