Why do we differentiate in physics and why twice?

[Physou]

I have a basic understanding of the reason why we look for derivative or integration in Physics, based on the water flow example, where integration is the process of accumulating the varying water flow rate "2x" , while we reverse to the water flow rate by differentiating " x squared " the integral of 2x. So I understand that in general we differentiate when we know the integration, ie the cumulative effect of a function but we want to know the function ? am I right ? given my limited knowledge I don't understand why we differentiate ( and also why twice ? ) in the picture attached

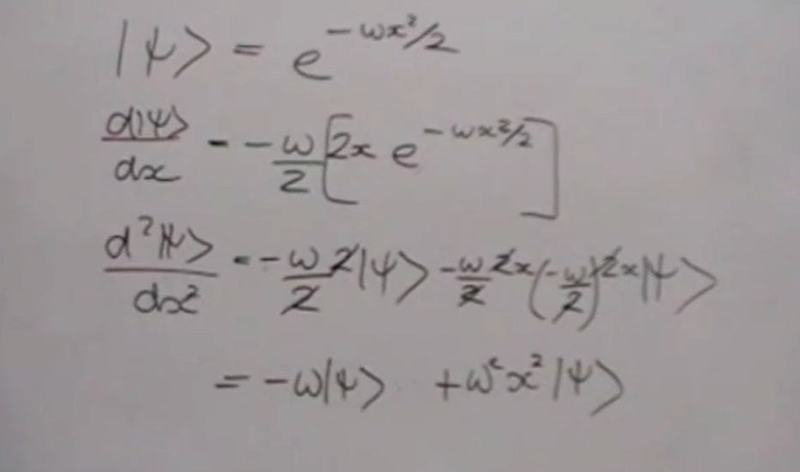. I will be very grateful for any help with basic terms. Thank you !

 

[Swamp Thing]

In this context, the first derivative tells you how fast $\psi$ would change as you move along the X axis. The second derivative quantifies the sense that $\psi$ changes "faster and faster" (or slower and slower) as you move along. These numbers happen to be important for quantum objects, because they are related to the momentum and kinetic energy. Their relationship (via Schroedinger's equation) governs how the object evolves in space and time, which in turn let's us predict the probabilities of various outcomes of mesurements/experiments.

This .. http://www.felderbooks.com/papers/psi.html .. is one of the many resources that I found useful when I was trying to understand this stuff.

 

[Physou]

Thank you so much for your explanation and also for the link .. there are many more hours of reading ahead of me !

 

[vanhees71]

First of all, this is an abuse of notation. A state ket doesn't depend on $x$. It's the wave function, i.e., the position representation of the state ket that depends on $x$:
$$\psi(x)=\langle x|\psi \rangle.$$
Now you have the wave function
$$\psi(x)=\exp(-\omega x^2/2),$$
and you take derivatives as usual. Your first derivative is correct. Using the chain rule you get
$$\psi'(x)=-\omega x \exp(-\omega x^2/2)=-\omega x \psi(x).$$
The 2nd derivative is then given by the product rule
$$\psi''(x)=-\omega \psi(x)-\omega x \psi'(x)=-\omega \psi(x)+\omega^2 x^2\psi(x).$$
So also your 2nd derivative is correct. So where is your problem?

In this case the motivation to do differentiation is that in the position representation, the momentum is represented by derivatives, i.e., (when using units with $\hbar=1$)
$$\hat{p} \psi(x)=-\mathrm{i} \psi'(x).$$
The Hamilton operator of the harmonic oscillator is given by
$$\hat{H}=\frac{\hat{p}^2}{2m}+\frac{m \omega^2}{2} \hat{x}^2.$$
In the position reprsentation the position operator is just multplication with $x$. Thus you get
$$\hat{H} \psi(x)=-\frac{1}{2m} \psi''(x)+\frac{m \omega^2}{2} x^2 \psi(x).$$
Now instead of the above used wave function, use
$$\Psi_0(x)=\exp \left (-\frac{m \omega x^2}{2} \right).$$
then you get
$$\hat{H} \Psi_0(x)=-\frac{1}{2m} [-m \omega \Psi_0+m^2 \omega^2 \Psi_0]+\frac{m \omega^2 x^2}{2} \Psi_0(x)=\frac{\omega}{2} \Psi_0(x),$$
which shows you that $\Psi_0$ is an eigenfunction of the Hamiltonian with eigenvalue $\omega/2$. In fact, it's the ground state of the harmonic oscillator!