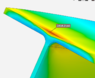
- #1
kravky
- 22
- 3
Hello,
i would like to ask You a question about difference in results between Euler-Bernoulli method of analysis of stress in short slender beam and 3D FEA method mentioned in ansys aim tutorial here: https://confluence.cornell.edu/pages/viewpage.action?pageId=33636829
The problem looks like this:
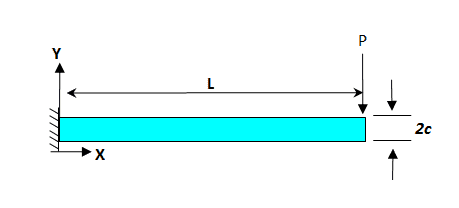
where P = 1000 lbf, L = 24 in, c = 4 in. P is applied force only in -y direction

Problem: The Result of simgaX (normal stress in x direction) after hand calculation (850psi) using Bernoullis model is two times smaller than result obtained using FEA in ANSYS (1800psi).
Here is hand calculation using Euler-Bernoulli theory:
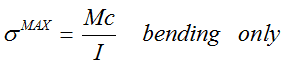
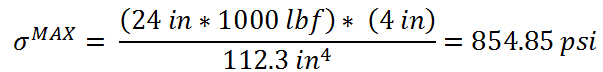
HOwever, as i mentioned, the result form ansys for sigmaX is 1833psi.
What is worng with that theory?
In that tutorial here: https://confluence.cornell.edu/pages/viewpage.action?pageId=3363682 It is mentioned that "substantial out-of-plane stresses (sigmaZ, simgaY) result in Poisson effects on the normal wall stress (sigmaX), increasing its value substantially".
I understand that sigmaZ (710psi according to ansys) is due to the fixation of this beam however sigmaZ is positive = its tensile. simgaX is also tensile so sigmaX should be REDUCED according to Poisson effect. And according to ANSYS it really is because overall equivalent stress (1400psi) is actually smaller than sigmaX (1800psi). (Its due to the fact that all stresses are tensile ( i talk about point above neutral axis)
But it is still much higher than simgaX of Bernoulli
https://ctrlv.cz/F1mf - this shows only representation of stresses
So the big difference in simgaX between Euler-Bernoulli (sigmaX=850) and 3D FEA ANSYS method (sigmaX=1800psi) can not be caused by out of plane stress.I would like to ask, why is the real value of sigmaX almost two times higher than it is according to Euler-Bernoulli beam theory?
Is it due to the fact, that beam is short and has it sth to do with shear stress?
What theory can be used to calculate analytically more accurately the value of sigmaX (i mean value close to the reality) ?
I know that simgaZ is zero according to euler and that it is not true, but it should decrease sigmaX and not increase it...
It seems so simple, so please answer me.
i would like to ask You a question about difference in results between Euler-Bernoulli method of analysis of stress in short slender beam and 3D FEA method mentioned in ansys aim tutorial here: https://confluence.cornell.edu/pages/viewpage.action?pageId=33636829
The problem looks like this:
where P = 1000 lbf, L = 24 in, c = 4 in. P is applied force only in -y direction
Problem: The Result of simgaX (normal stress in x direction) after hand calculation (850psi) using Bernoullis model is two times smaller than result obtained using FEA in ANSYS (1800psi).
Here is hand calculation using Euler-Bernoulli theory:
HOwever, as i mentioned, the result form ansys for sigmaX is 1833psi.
What is worng with that theory?
In that tutorial here: https://confluence.cornell.edu/pages/viewpage.action?pageId=3363682 It is mentioned that "substantial out-of-plane stresses (sigmaZ, simgaY) result in Poisson effects on the normal wall stress (sigmaX), increasing its value substantially".
I understand that sigmaZ (710psi according to ansys) is due to the fixation of this beam however sigmaZ is positive = its tensile. simgaX is also tensile so sigmaX should be REDUCED according to Poisson effect. And according to ANSYS it really is because overall equivalent stress (1400psi) is actually smaller than sigmaX (1800psi). (Its due to the fact that all stresses are tensile ( i talk about point above neutral axis)
But it is still much higher than simgaX of Bernoulli
https://ctrlv.cz/F1mf - this shows only representation of stresses
So the big difference in simgaX between Euler-Bernoulli (sigmaX=850) and 3D FEA ANSYS method (sigmaX=1800psi) can not be caused by out of plane stress.I would like to ask, why is the real value of sigmaX almost two times higher than it is according to Euler-Bernoulli beam theory?
Is it due to the fact, that beam is short and has it sth to do with shear stress?
What theory can be used to calculate analytically more accurately the value of sigmaX (i mean value close to the reality) ?
I know that simgaZ is zero according to euler and that it is not true, but it should decrease sigmaX and not increase it...
It seems so simple, so please answer me.