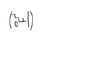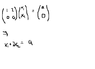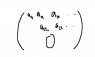The rank of a matrix is defined as the dimension of the range, which corresponds to the number of pivot points in its reduced row echelon form. Both the original matrix and its reduced form share the same rank because they represent the same linear transformation, preserving the relationships between their columns. The columns with pivot points form a basis for the range, while columns without pivot points can be expressed as linear combinations of those with pivots. The range consists of all vectors that can be represented as Ax for some x, confirming that the rank reflects the number of independent directions in the vector space. Understanding these concepts clarifies why the rank equals the number of pivot points.