Would including the true/known y-intercept in my dataset be "overfitting"?

[FactChecker]

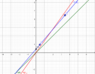
Below is a simple example to illustrate the pros and cons of the two regression models.
Suppose: Suppose the true physics without any random behavior is the green (truth) line Y=X, and suppose we know from theory that it goes through (0,0). Two sample data points, $S_1$ and $S_2$ include some random behavior which puts them above the truth line and forces the typical regression (blue line, $regr_1$) to have a nonzero Y-axis intercept at point Int. Suppose the restricted red regression line ($reg_2$ through (0,0)) is calculated because we theoretically know that Y=0 when X=0 if there is no random behavior.

Then: The red line gives better estimates near (0,0) and worse estimates farther away. Also, its slope is worse. But it has one advantage when challenged by skeptical people -- it is correct at the Y-intercept, where a theoretical answer is known. I would prefer to avoid using the blue line as my model when it is undeniably wrong at the Y-intercept. But that depends on how the model is used. If accuracy far from the Y-intercept is more important than accuracy near the Y-intercept, then you may prefer the model that ignores the known theory of the Y-intercept value.

 

[Dale]

With this information in mind, do you still agree to include the intercept in the measured data points and fit normally with no restrictions?

Yes, but only if you actually measure the intercept. So it should be a real data point treated just like any other real data point.

 

[Dale]

I would not recommend ignoring the theoretical known value, no matter how it changes the statistical results. I see no reason to prefer accurate statistical measures of a known invalid model. I would prefer modified statistical measures of a known valid model.

That can be done, but it has to be a very explicit and convincing argument. Personally, when I see a statistical model done without an intercept I am instantly highly suspicious. The burden of proof is on the scientist much more stringently, and frankly in some infamous papers where I have seen this done it was done poorly and rendered the conclusion completely unbelievable.

So overall, my opinion is opposite yours. I would rather use a standard and reasonable statistical process and look at the fitted intercept as a check on the quality of the data and the model.

 

[FactChecker]

That can be done, but it has to be a very explicit and convincing argument.

I agree completely with that. The theoretical reason behind the Y-intercept of 7 must be hard, solid science. If there is any doubt, the standard regression intercept should be allowed.

 

[Dale]

@fahraynk FYI both @FactChecker And I agree about this point also

If that is not a measured experimental data point, then it is a theoretical point. If it's a theoretical true value, why only include it once? Why not two or three times? Or 20 times? Pretending that the theoretical intercept is an experimental sample data point is the wrong way to go.

So don’t make a fictitious data point.

 

[FactChecker]

That can be done, but it has to be a very explicit and convincing argument. Personally, when I see a statistical model done without an intercept I am instantly highly suspicious. The burden of proof is on the scientist much more stringently, and frankly in some infamous papers where I have seen this done it was done poorly and rendered the conclusion completely unbelievable.

So overall, my opinion is opposite yours. I would rather use a standard and reasonable statistical process and look at the fitted intercept as a check on the quality of the data and the model.

I think that I have to concede that your approach is the wiser approach. Forcing the Y-intercept to a particular value would only be appropriate if there is indisputible consensus based on science.

 

[Rap]

The problem is stated mathematically as:
ε²=Σ(m x_i+b-y_i)²
b=7
Minimizing the mean square error (ε²)
dε²/dm = 0 = Σ(m x_i+b-y_i) x_i
Solve above for m and that’s your fitting equation, y=mx+7. m will be expressed entirely in terms of known quantities with a guaranteed intercept of 7.