SUMMARY
The discussion centers on the interpretation of the equation presented by Zee in "QFT Nut," specifically regarding the expression involving the divergence of a vector field, denoted as ##(\partial_i A_i)##. Participants clarify that this expression vanishes under certain gauge conditions and emphasize the importance of the product rule in quantum field theory. The conversation highlights the confusion caused by Zee's notation compared to more straightforward explanations found in texts like Griffith's "Intro to Electrodynamics." The corrected expression for the momentum operator acting on a wave function is presented as $$(\partial_i A_i + A_i \partial_i) X = 2 A_i \partial_i X$$, illustrating the application of the product rule.
PREREQUISITES
- Understanding of quantum field theory (QFT) principles
- Familiarity with vector calculus, particularly divergence
- Knowledge of operator notation in quantum mechanics
- Experience with gauge theories and their implications
NEXT STEPS
- Study the product rule in quantum mechanics and its applications
- Review Griffith's "Intro to Electrodynamics" for clearer explanations of similar concepts
- Explore gauge theories in quantum field theory for deeper insights
- Learn about the implications of operator actions on wave functions in QFT
USEFUL FOR
This discussion is beneficial for physics students, quantum field theorists, and educators seeking clarity on complex notation and concepts in quantum mechanics, particularly those related to gauge theories and operator algebra.
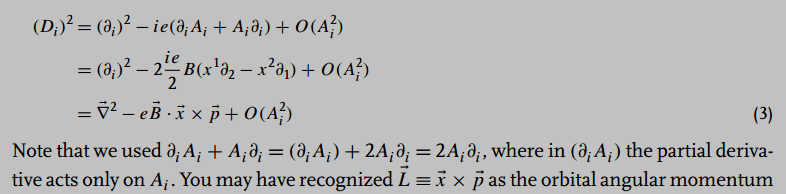
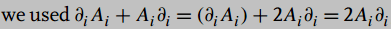 ??
??