Discussion Overview
The discussion revolves around the interpretation of a specific equation presented in Zee's work on quantum field theory (QFT), particularly focusing on the notation and implications of the equation as it relates to the divergence of a vector field and its application in the context of momentum operators and wavefunctions.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants suggest that the term ##(\partial_i A_i)## represents the divergence of the vector field A, which may vanish under certain gauge conditions considered by Zee.
- There is a question regarding what the partial derivative acts upon, with some participants proposing that it could act on a wavefunction in addition to A.
- One participant proposes an alternative expression for the equation, applying the product rule to clarify the relationship between the terms involved.
- Another participant expresses confusion over Zee's notation, suggesting that it complicates rather than clarifies the concepts, contrasting it with a clearer explanation provided by another participant.
- A later reply draws a parallel between the equation in question and a well-known relation in quantum mechanics, indicating a broader context for understanding the derivation.
- There are multiple suggestions for rewriting the equation to enhance clarity, with some participants pointing out missing components in earlier expressions.
Areas of Agreement / Disagreement
Participants express differing views on the clarity and utility of Zee's notation, with some finding it confusing while others defend its generalization. There is no consensus on the interpretation of the equation or the best way to express it.
Contextual Notes
Participants note potential ambiguities in the notation and the assumptions underlying the expressions, particularly regarding the application of derivatives and the roles of wavefunctions.
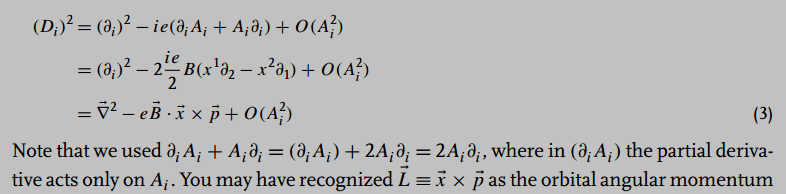
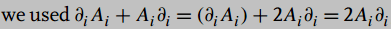 ??
??