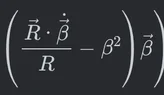anuttarasammyak's latest activity
-
 anuttarasammyak replied to the thread I Infinite number of spatial dimensions (maybe also time dimensions).We are familiar with countable infinite dimension Hilbert space in QM. You may be able to get some hint for your problem from it.
anuttarasammyak replied to the thread I Infinite number of spatial dimensions (maybe also time dimensions).We are familiar with countable infinite dimension Hilbert space in QM. You may be able to get some hint for your problem from it. -
 anuttarasammyak replied to the thread I EPR revisited.Thank you @PeterDonis. I should be somewhat satisfied to know that studies are going on.
anuttarasammyak replied to the thread I EPR revisited.Thank you @PeterDonis. I should be somewhat satisfied to know that studies are going on. -
 anuttarasammyak replied to the thread Help with derivation of electric field of a moving charge.The first term has dimension of T^-1 though it should be non dimensional. You should investigate its derivation.
anuttarasammyak replied to the thread Help with derivation of electric field of a moving charge.The first term has dimension of T^-1 though it should be non dimensional. You should investigate its derivation. -
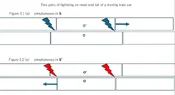
 anuttarasammyak replied to the thread I Relativity of simultaneity in actuality.The author explains the figures saying "the point of view of S(or S′)". Therefore, there is a possibility that readers may...
anuttarasammyak replied to the thread I Relativity of simultaneity in actuality.The author explains the figures saying "the point of view of S(or S′)". Therefore, there is a possibility that readers may... -
 anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I see. “The moving inertial frame against the original IFR” would eliminate those cases.
anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I see. “The moving inertial frame against the original IFR” would eliminate those cases. -
 anuttarasammyak reacted to wrobel's post in the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature? with
anuttarasammyak reacted to wrobel's post in the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature? with Like.
I was hoping that the name existed. :( The moving frame can for example rotate and its different points can have different velocities...
Like.
I was hoping that the name existed. :( The moving frame can for example rotate and its different points can have different velocities... -
 anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I do not think so. In the text, "(absolute) velocity of the moving frame" is better.
anuttarasammyak replied to the thread A Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?.I do not think so. In the text, "(absolute) velocity of the moving frame" is better. -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.An example of my point. Say light is passing on element ##dx^\mu##, i.e., $$ g_{\mu\nu}dx^\mu dx^\nu = 0 $$ After variation of metric $$...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.An example of my point. Say light is passing on element ##dx^\mu##, i.e., $$ g_{\mu\nu}dx^\mu dx^\nu = 0 $$ After variation of metric $$... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Yes. For $$g_{\mu\nu}= g_{\mu\alpha} g_{\beta\nu} g^{\alpha\beta},\ g^{\mu\alpha} g_{\alpha\nu}=\delta^\mu_\nu...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.Yes. For $$g_{\mu\nu}= g_{\mu\alpha} g_{\beta\nu} g^{\alpha\beta},\ g^{\mu\alpha} g_{\alpha\nu}=\delta^\mu_\nu... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.$$\bar{g}_{\mu\nu} - g_{\mu\nu} = \delta g _{\mu\nu} = - \delta \bar{g}_{\mu\nu} $$ ##\bar{g}_{\mu\nu}## is a tensor in the world where...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.$$\bar{g}_{\mu\nu} - g_{\mu\nu} = \delta g _{\mu\nu} = - \delta \bar{g}_{\mu\nu} $$ ##\bar{g}_{\mu\nu}## is a tensor in the world where... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.I agree that index raise- lower operation should be done using one same, old or new, metric for all the indexes of all the entities in...
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.I agree that index raise- lower operation should be done using one same, old or new, metric for all the indexes of all the entities in... -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.My bad. I withdraw it.
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.My bad. I withdraw it. -
 anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.To me the point is two metrics: original and varied. In varied metric world what kind of things or relations remain and what does not ?
anuttarasammyak replied to the thread A Is the variation of the metric ##\delta g_{\mu\nu}## a tensor?.To me the point is two metrics: original and varied. In varied metric world what kind of things or relations remain and what does not ?