Recent content by mdb71
-
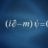
Graduate Smart Algebra of Exp. on Pg 191 of Peskin & Schroeder
Just solved; I'll post the scan of the working in the next few days just for reference as it is quite an annoying passage. Other than that, feel free to post your answers, it is an opportunities to see some smart tricks at play- mdb71
- Post #4
- Forum: High Energy, Nuclear, Particle Physics
-
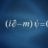
Graduate Smart Algebra of Exp. on Pg 191 of Peskin & Schroeder
The argument of u is p, not p'. What do you mean what is their relation? They are spinors coming from the vertices which the propagators are attached. However, this is irrelevant; what is important here is the on shell identity - coming from the Dirac equation - by which we may simplify terms...- mdb71
- Post #3
- Forum: High Energy, Nuclear, Particle Physics
-
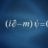
Graduate Smart Algebra of Exp. on Pg 191 of Peskin & Schroeder
Hi all, I have a problem working out the algebra of the following expression in Peskin & Schroeder in a smart way to give the result. It is on page 191, regarding the numerator of the vertex correction function. We want to get from the LHS to the RHS of the following expression...- mdb71
- Thread
- Algebra Peskin Schroeder
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
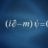
Undergrad How Peskin & Schroeder simplified this horrible product of bilinears?
Thanks a lot, appreciate. Got it now, I was still getting used to it.- mdb71
- Post #6
- Forum: Quantum Physics
-
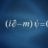
Undergrad How Peskin & Schroeder simplified this horrible product of bilinears?
Hey good question. This comes down to a few basic observations about sigma matrices. First of all, we note $$ (i\sigma ^2)_{\alpha\beta} = \epsilon_{\alpha\beta}. $$ Next we rephrase the statement of the problem in a slightly more illuminating form: $$ (i\sigma^2 \sigma^{\mu})_{\alpha\beta}=...- mdb71
- Post #4
- Forum: Quantum Physics