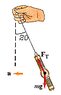Estimate takeoff speed of aircraft

[physicsss]

Francesca, who likes physics experiments, dangles her watch from a thin piece of string while the jetliner she is in takes off from Dulles Airport. (see pic. attached) She notices that the string makes an angle of 20° with respect to the vertical while the aircraft accelerates for takeoff, which takes about 14.5 seconds. Estimate the takeoff speed of the aircraft.

I have no idea where to start...

 

[HallsofIvy]

I have a slight problem with this: obviously the airplane is climbing (at a steep angle in my experience!) but nothing is said about the angle of climb. If we take the angle of the watch to be from the "airplane's vertical" (vertical to the floor of the airplane) we still can't calcuate the angle at which gravity asks. Conversely, if we take the angle of the watch to be from "true vertical", we don't know which way the "force" due to the acceleration of the airplane is directed.

I will assume we are talking about the acceleration along the runway so that the angle of climb is 0: the force due to gravity is downward and the acceleration of the airplane is forward, perpendicular to gravity.

You know the downward force on the watch is mg and you know the force on the watch (backward) due to the airplanes acceleration, a, is ma. Write those as vectors and sum. What must a be in order that the resultant vector is 20 degrees to the vertical? After you know a, it will be easy to find the final velocity (the takeoff speed! Yes, the problem was talking about acceleration down the runway!).

 

[physicsss]

nm...got it

 

[Fanman22]

I have a slight problem with this: obviously the airplane is climbing (at a steep angle in my experience!) but nothing is said about the angle of climb. If we take the angle of the watch to be from the "airplane's vertical" (vertical to the floor of the airplane) we still can't calcuate the angle at which gravity asks. Conversely, if we take the angle of the watch to be from "true vertical", we don't know which way the "force" due to the acceleration of the airplane is directed.

I will assume we are talking about the acceleration along the runway so that the angle of climb is 0: the force due to gravity is downward and the acceleration of the airplane is forward, perpendicular to gravity.

You know the downward force on the watch is mg and you know the force on the watch (backward) due to the airplanes acceleration, a, is ma. Write those as vectors and sum. What must a be in order that the resultant vector is 20 degrees to the vertical? After you know a, it will be easy to find the final velocity (the takeoff speed! Yes, the problem was talking about acceleration down the runway!).

Ok, I used the vectors, 9.8 and "a" with my angle being 25. I got 21m/s^2 for my a. My time was 10seconds so I used the formula Vf=Vi + at and got a final velocity of 210m/s...and the program says I'm wrong...how?

 

[Integral]

What do you get for the 20 angle specified in the problem?

 

[Fanman22]

If I use an angle of 20degrees and a t=14.5, then I get 390m/s.
Basically, all I'm doing is 9.8/tan(angle)=a , then a*t=Final velocity.

 

[dextercioby]

It's the other way around,as u check in the right triangle where u can use "tan"...
$$a=g\tan 20$$°

Daniel.

 

[Fanman22]

AHHHHHHHHHHHH I hate when its something so simple LOL

 

[Fanman22]

hey wait a second...tan = opposite / adjacent. The opposite side is the 9.8 (b/c gravity is downwards) and the adjacent side is the "a". So tan20=9.8/a, not a/9.8

What am I missing?