SUMMARY
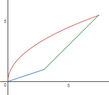
The discussion focuses on expressing integrals to find the area of a region bounded by the curves defined by the equations \(y=2\sqrt{x}\), \(3y=x\), and \(y=x-2\). The area \(A\) is calculated using two integrals: \(A = \int_0^3 (2\sqrt{x} - \frac{x}{3}) \, dx + \int_3^{4+2\sqrt{3}} (2\sqrt{x} - (x-2)) \, dx\). Additionally, the possibility of expressing the area using double integrals is explored, leading to the formulation \(A=\int_0^3\int_{x-2}^{2\sqrt{x}}\,dy\,dx+\int_3^{4+2\sqrt{3}}\int_{\frac{x}{3}}^{2\sqrt{x}}\,dy\,dx\). The discussion also touches on the challenges of expressing the area as a single integral and the potential use of polar coordinates.
PREREQUISITES
- Understanding of integral calculus, specifically area under curves.
- Familiarity with the equations of curves and their intersections.
- Knowledge of double integrals and their applications in calculating area.
- Basic understanding of polar coordinates and their conversion from Cartesian coordinates.
NEXT STEPS
- Study the method of finding area between curves using definite integrals.
- Learn about double integrals and their applications in multivariable calculus.
- Explore the conversion of Cartesian coordinates to polar coordinates for area calculations.
- Investigate the use of numerical methods for approximating areas under complex curves.
USEFUL FOR
Students and educators in calculus, mathematicians interested in integral applications, and anyone involved in advanced geometry or multivariable calculus.