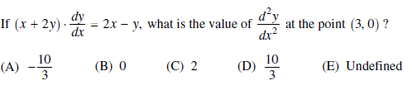Discussion Overview
The discussion revolves around the calculation of the second derivative from a given first derivative equation in the context of an AP Calculus exam problem. Participants explore the steps involved in deriving the second derivative and evaluate it at specific points, while also referencing answer choices from the exam.
Discussion Character
- Mathematical reasoning
- Homework-related
- Debate/contested
Main Points Raised
- One participant suggests starting the derivation by dividing both sides of the equation $$\dfrac{dy}{dx}=\dfrac{2x-y}{x+2y}$$.
- Another participant provides the expression for the second derivative, $$\dfrac{d^2y}{dx^2} = \dfrac{(x+2y) \left(2 - \frac{dy}{dx} \right) - (2x-y)\left(1+2\frac{dy}{dx}\right)}{(x+2y)^2}$$, noting a specific value for $$\dfrac{dy}{dx}$$ at the point (3,0).
- Some participants discuss substituting specific values of $$x$$ and $$y$$ into the second derivative expression, leading to calculations that yield $$-\frac{10}{3}$$.
- There is a correction regarding the answer choice, indicating that the initial assumption of the answer being D is incorrect, prompting a reevaluation of the answer choices.
- A later reply presents an alternative derivation approach, leading to the same conclusion of $$\frac{d^2y}{dx^2}=-\frac{10}{3}$$.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct answer choice, as there are conflicting interpretations of the results and the answer options provided in the exam.
Contextual Notes
There are unresolved aspects regarding the derivation steps and the implications of the answer choices, which may depend on the definitions and interpretations of the problem presented.