3D geometry parallelepiped problem

[geoffrey159]

Homework Statement

[/B]
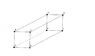
Given a rectangular parallelepiped ABCDEFGH, the diagonal [AG] crosses planes BDE and CFH in K and L. Show K and L are BDE's and CFH's centres of gravity.

I think I have understood the problem, could you verify my demo please ? Thanks

Homework Equations

The Attempt at a Solution

Let us call $G_1$ and $G_2$ BDE's and CFH's center of gravity.

$\vec{AG} = \vec{AB} + \vec{AD} + \vec{AE} = 3 \vec{AG_1}$

So $A,G_1, G$ are aligned and $G_1$ belongs to plane BDE so we must have $K = G_1$

Then

$3 \vec{AG_2} = \vec{AC} + \vec{AF} + \vec{AH} = \vec{AB} + \vec{BC} + \vec{AE}+\vec{EF} + \vec{AD} + \vec{DH} = \vec{AG} + \vec{BC} + \vec{EF}+\vec{DH} = 2\vec{AG}$

So, similarly, $A,G_2, G$ are aligned and $G_2$ belongs to plane CFH so we must have $L = G_2$

Furthermore, $K$ and $L$ are at the third and two third of the diagonal.

 

[jedishrfu]

It would help if you provided a picture of your regular parallelepiped with vertices labeled.

 

[geoffrey159]

Hi, here is the picture