4-colours theorem can be proved visually

[Adel Makram]

TL;DR

Visual proof of the 4-colour theorem.

The 4-colour theorem states that the maximum number of colours required to paint a map is 4.
The proof requires exhaustive computation with a help of a computer.

But I thought that one can visually prove the theorem in the following way;

If one replaces the map with a graph where each region with a different colour is represented by a vertex and the two adjacent regions represented by an edge between the vertices. Then, the maximum number of vertices in any complete planar local graph where every two vertices are connected and no crossing of the edges is allowed must be 4.

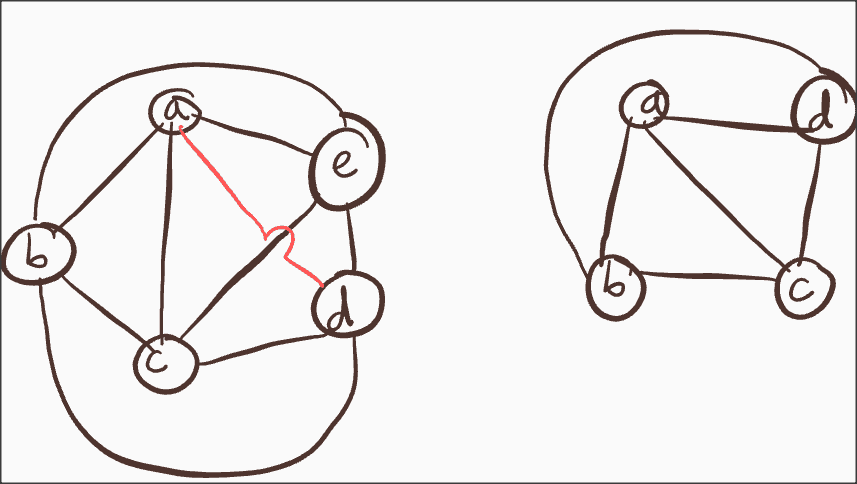
For example, the picture on the right shows that all vertices (a,b,c,d) are connected and therefore corresponds to the fact that the maximum number of allowed colours is 4.
While the picture on the left shows that it is impossible to get 5 colours to paint the map because the regions represented by the vertices (a) and (d) in the map will not be adjacent to each other (no edge connects (a) and (d) exits without crossing the other edges).

 

[Office_Shredder]

The theorem is a lot deeper than that. If you take blocks of four nodes that you have painted, and then got connect all of them to make a larger graph, how do you know you can do that without being forced to connect two nodes that you already painted the same color?

 

[Vanadium 50]

IBTL.

It's not clear what you proved, since you haven't expressed it in the language of proofs, but it appears that you have found one possibility that requires four colors. That's a very different thing than proving the theorem.

 

[mfb]

You have only (somewhat) shown that you don't need 5 colors for maps with 5 regions/vertices (mathematically: because the complete graph K_5 is not planar, i.e. can't correspond to a map). You haven't shown that this applies to arbitrarily large maps. They won't be complete graphs, obviously, but you can create graphs where every vertex has at least four connections, so you cannot easily remove one vertex from consideration.

If it would be that simple people wouldn't have needed a computer...

 

[Adel Makram]

The theorem is a lot deeper than that. If you take blocks of four nodes that you have painted, and then got connect all of them to make a larger graph, how do you know you can do that without being forced to connect two nodes that you already painted the same color?

Because colouring a map requires only local rules, I believe. When this set of 4-nodes becomes part of a larger graph, one can treat each local set of 4-nodes separately without affecting other remote parts of the graph.

 

[mfb]

You need to prove that... (if it is correct at all, which I doubt).

 

[Adel Makram]

You need to prove that... (if it is correct at all, which I doubt).

Do I need to prove that colouring a map requires local rule?
What I am trying to say is if the 4-colours theorem is false, then the maximum number of required colours should be at least 5. But the picture shows that can not be the case, therefore the theorem must be true.

 

[Office_Shredder]

What does "local rules" mean?

If I just show you 4 vertices at a time, do you think you can pick colors of those vertices such that at the end you have properly colored the graph? I don't think you can, and am happy to go through an example with you.

 

[Vanadium 50]

Do I need to prove that colouring a map requires local rule?

You need to prove something, as in write a proof. Not just make the assertion again and again.

 

[Adel Makram]

What does "local rules" mean?

If I just show you 4 vertices at a time, do you think you can pick colors of those vertices such that at the end you have properly colored the graph? I don't think you can, and am happy to go through an example with you.

Instead, can you show me a part of any graph where the maximum number of distinct colors of the adjacent vertices is 5?

 

[Vanadium 50]

Instead, can you show me a part of any graph where the maximum number of distinct colors of the adjacent vertices is 5?

Irrelevant. That you have one graph that can be colored with four colors does not prove the Four-Color Theorem.

You have proven nothing whatever. For the third time, I request that you use the language of proofs - a step-by-step logical argument, with lemmas if necessary. I am beginning to doubt that you can even correctly state the Four-Color Theorem, because if you have proven anything at all (which I don't think you have), the Four-Color Theorem isn't it.

 

[MidgetDwarf]

I think that maybe reading about how mathematical proofs work would be the best step to understanding that what you offered in your initial proof is not really a mathematical proof.

 

[mfb]

What I am trying to say is if the 4-colours theorem is false, then the maximum number of required colours should be at least 5.

That is trivial as 5 is the smallest integer larger than 4.

But the picture shows that can not be the case

It doesn't do that. It just shows that one specific map is not a counterexample.

 

[Adel Makram]

I will try here to put it in a semiformal way;

The map of regions n is isomorphic to a graph of vertices n where each region of distinct colour is represented by a vertex of a different colour.

Adjcaney: two regions in the map are adjacent if there is an edge connecting the corresponding 2 vertices representing these regions on the map.

The minimum requirement: We are trying to colour the map with a minimum number of colors such that no adjacent regions have the same colours.

Suppose that we locate 5 regions in the map which are adjacent and satisfying the minimum requirement.

Then that region is isomorphic to a planar graph of K5.

But Kuratowski's theorem states that a finite graph is planar if and only if it does not contain a subgraph that is homeomorphic to K5

This contradicts the proposal that we can find that a patch of the map with adjacent regions of 5 different colours.

 

[Office_Shredder]

You are still missing the point. You can have for example a graph of 8 vertices such that any five vertices can be colored with four colors, but you can't combine all the colorings of the 5 vertex sections in a consistent way (there are 56 of them!)

Do you think that if I give you a graph and only show you chunks of five vertices at a time, that you can correctly color the whole graph?

 

[Adel Makram]

You are still missing the point. You can have for example a graph of 8 vertices such that any five vertices can be colored with four colors, but you can't combine all the colorings of the 5 vertex sections in a consistent way (there are 56 of them!)

Do you think that if I give you a graph and only show you chunks of five vertices at a time, that you can correctly color the whole graph?

You can give me any map with any number of regions, but I think when 5 colors can not satisfy the minimum requirement mentioned above at any subgraph then this is equivalent to the 4 colors theorem.

Or put it in this way; there is no subgraph that requires 5 colors across the entire graph.

If there is no local patch of the graph requiring 5 colors (guaranteed by Kuratowski's theorem), then the entire graph does not require it either.

 

[Adel Makram]

I think I just now understood what you meant by coloring. When I say 5 colors, I mean those particular 5 colors; say (red, green, blue, yellow, orange).
Suppose we have a scanning device that walks across the map and is programmed such that it will beep when it finds a region of the map homeomorphic to K5. I claim that we will never hear the beep.

 

[willem2]

Suppose that we locate 5 regions in the map which are adjacent and satisfying the minimum requirement.

Then that region is isomorphic to a planar graph of K5.

But Kuratowski's theorem states that a finite graph is planar if and only if it does not contain a subgraph that is homeomorphic to K5

This contradicts the proposal that we can find that a patch of the map with adjacent regions of 5 different colors.

Note that if you have to prove that A implies C, and you at first prove A implies B and then B implies C,
and someone produces a counterexample where B is true, but C is false, then your proof must be wrong.

Here A is: the graph G is planar.
B: the graph G does not contain K⁵
C: the graph G can be colored with 4 colors.

Now for the counterexample. There are maps that do not even contain a triangle, that need an arbitrary number of colors. Of course these are non-planar.
These are Mycielsky graphs: https://en.wikipedia.org/wiki/Mycielskian
For every graph G with N vertices and E edges, Mycielsky defines a graph with 2N+1 vertices and 3E+N edges that has G as a subgraph, but contains no new triangles, and needs one more color.
If your starting graph has no triangles, your new graph also will contain no triangles.

If you start with a graph with 2 vertices and one edge and use the process 3 times, you get a graph with 23 vertices and 71 edges that needs 5 colours.

There's an image at page 48 of this paper
http://webdocs.cs.uAlberta.ca/~hayward/theses/erik.pdf/

 

[Adel Makram]

Note that if you have to prove that A implies C, and you at first prove A implies B and then B implies C,
and someone produces a counterexample where B is true, but C is false, then your proof must be wrong.

Here A is: the graph G is planar.
B: the graph G does not contain K⁵
C: the graph G can be colored with 4 colors.

Interesting graphs thank you.

Do you mean a Planar graph G that contains no K⁵ can be colored with a minimum of more than 4 colors?

 

[Office_Shredder]

No, the claim is simply that no $K^5$ is not enough to prove that you can do it in four colors.

 

[mfb]

Suppose that we locate 5 regions in the map which are adjacent and satisfying the minimum requirement.

The "minimum requirement" applies to the whole graph, not just 5 regions. The minimum for a given subgraph can be smaller. That's trivial.

 

[Office_Shredder]

Probably the best example is you might guess something like, if a graph has no triangles then it can be colored with 2 colors, because every set of 3 vertices can be colored correctly. But if you just take the graph that's shaped like a pentagon, you can't actually color it using two colors. Any odd numbered cycle cannot be colored with only two colors - so coloring with two colors is not something you can do with a "local rule"

If it's not obvious after that what we are trying to say, I'm not really sure how else to say it. But you should probably at least feel like you're probably wrong, since generations of professionals were all aware of the relationship between $K^5$ graphs and being planar, and none of them thought that was a proof. So please, instead of asking us to explain from scratch again why you haven't proven it, take the time to try to understand the posts already explaining why it's not a proof, and if a specific thing confuses you ask about that.