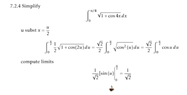SUMMARY
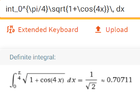
The discussion focuses on integrating the function $$\int_0^{\pi/4} \sqrt{1+\cos(4x)} \, dx$$ using substitution and trigonometric identities. The substitution $u=2x$ simplifies the integral to $$\frac{1}{2} \int_0^{\pi/2} \sqrt{1+\cos(2u)} \, du$$. By applying the double angle identity, the integral further reduces to $$\frac{\sqrt{2}}{2} \int_0^{\pi/2} \cos{u} \, du$$, ultimately yielding the result $$\frac{\sqrt{2}}{2}$$. The key takeaway is the importance of resetting limits during substitution in definite integrals.
PREREQUISITES
- Understanding of definite integrals
- Familiarity with trigonometric identities, specifically the double angle identity
- Knowledge of substitution methods in calculus
- Basic skills in evaluating integrals involving square roots and trigonometric functions
NEXT STEPS
- Study the application of the substitution method in definite integrals
- Learn about trigonometric identities and their use in integration
- Explore advanced integration techniques, including integration by parts
- Practice problems involving integrals of the form $$\int \sqrt{a + b \cos(kx)} \, dx$$
USEFUL FOR
Students and educators in calculus, particularly those focusing on integration techniques and trigonometric functions. This discussion is beneficial for anyone looking to deepen their understanding of integration methods and their applications in solving definite integrals.