A aerialist on a high platform holds on to a trapeze attached to a sup

  • Thread starter Thread starter cmkc109
  • Start date Start date
  • Tags Tags
    Platform
Click For Summary
SUMMARY

The discussion focuses on calculating the angle θ that a trapeze cord makes with the vertical when an aerialist swings down and releases the trapeze. The initial setup involves an 8.2-meter cord making a 39.8-degree angle with the vertical before the jump. The calculations provided lead to an angle of 32.2 degrees, derived from the cosine function. The confusion arises regarding the initial position of the cord and the interpretation of the lengths involved in the trigonometric calculations.

PREREQUISITES
  • Understanding of basic trigonometry, specifically cosine functions.
  • Familiarity with the concepts of angles and vertical displacement in physics.
  • Knowledge of the relationship between angles and lengths in right triangles.
  • Ability to interpret and analyze geometric figures related to physics problems.
NEXT STEPS
  • Review trigonometric functions and their applications in physics problems.
  • Study the principles of pendulum motion and angular displacement.
  • Learn how to analyze forces and angles in static and dynamic systems.
  • Examine the geometry of triangles in relation to real-world applications, particularly in aerial performances.
USEFUL FOR

Students studying physics, particularly those focusing on mechanics and trigonometry, as well as educators looking for examples of real-world applications of these concepts.

cmkc109
Messages
103
Reaction score
0

Homework Statement



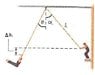
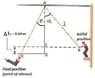
A aerialist on a high platform holds on to a trapeze attached to a support by a 8.2-m cord. Just before he jumps off the platform, the cord makes an angle α of 39.8deg with the vertical. He jumps, swings down, then back up, releasing the trapeze at the instant it is 0.64 m below its initial height. Calculate the angle θ that the trapeze cord makes with the vertical at this instant.

Homework Equations



cos(theta) = A/H

The Attempt at a Solution



So I found the solution online.
8.2 cos 39.8 = 6.3
6.3 + 0.64 =6.94
cos ^-1 (6.94 / 8.2) = 32.2 deg

However I am not understanding it at all. I don't understand where is the initial position, when the rope is vertical or when the guy is holding on to it?
I have attached the picture , can someone label on the picture or explain it please?

My understanding is, the middle is 8.2m , the right rope is 6.3m, and the left rope is 6.94m
but then the calculation doesn't really make sense.
since if the middle is 8.2, to find l, u should do cos 39.8 = 8.2 / l, and l will be 10.67 instead.
 

Attachments

  • swing.jpg
    swing.jpg
    8.8 KB · Views: 2,406
Physics news on Phys.org
The length of the rope is ##l## = 8.2 m. The length of the rope does not change.

Examine some of the triangles shown in the attached figure.
 

Attachments

  • Trapeze.jpg
    Trapeze.jpg
    11.9 KB · Views: 3,138
Last edited:
very helpful, thank you very much.
 

Similar threads

Swing Higher on Circus Trapeze: Solve Physics Problem
  • · Replies 1 ·
Replies
1
Views
6K