A Car on a Banked Curve Moving in Uniform Circular Motion

[RoboRaptor]

Homework Statement

A 1050-kg car rounds a curve of radius 72m banked at an angle of 14°. If the car is traveling at 85 km/h, will a friction force be required? If so, how much and in what direction?

Relevant Equations

Centripetal Force = (m*v^2)/R
Normal Force = Cos(x) * mg
Sin(x) = opp/hyp
Cos(x) = adj/hyp
g = 9.8m/s^2

First I figured out the normal force being exerted on the car using the equation above.
Cos(40°)*(1050*9.8) = 7883N
Next, I tried to find out the horizontal component of the normal force by doing:
Cos(50) * 7883 = 5067N
I figured out the angle by using certain geometrical properties.

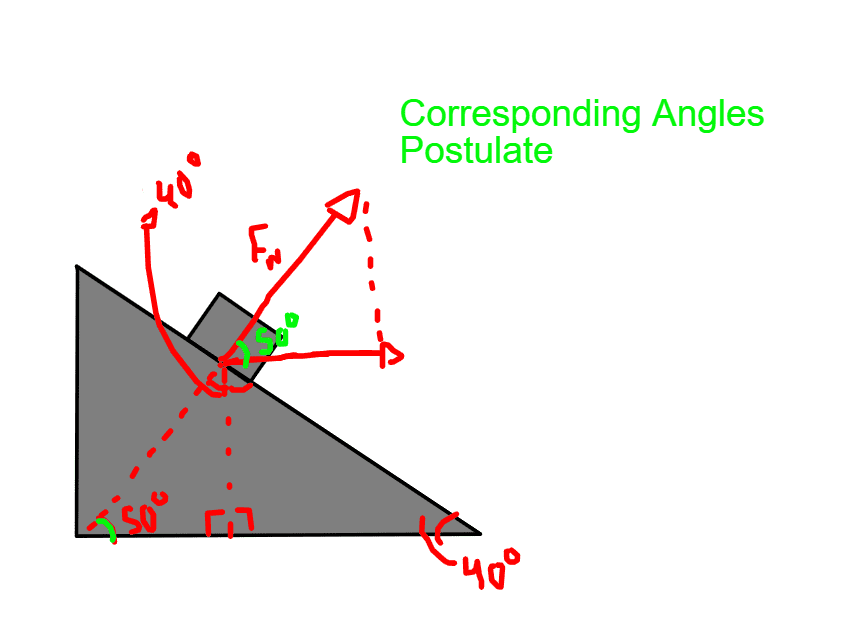
Next, I found the Centripetal Force using its corresponding equation:
F = 1050 * (23.6^2/72) = 8122 N
(I found 23.6 by dividing 85000 by 3600)
I figured out that the horizontal component of the Normal Force is not enough to give the object its circular motion so I found the difference between it and the Centripetal Force which gave me around 3055 more N needed to make the car go in a uniform circular motion.
Here is where I'm unsure of what to do. Will the frictional force of the car point directly to the center of the circular motion or will it point down towards the direction of the ramp?
Here are some pictures to better illustrate my doubts:

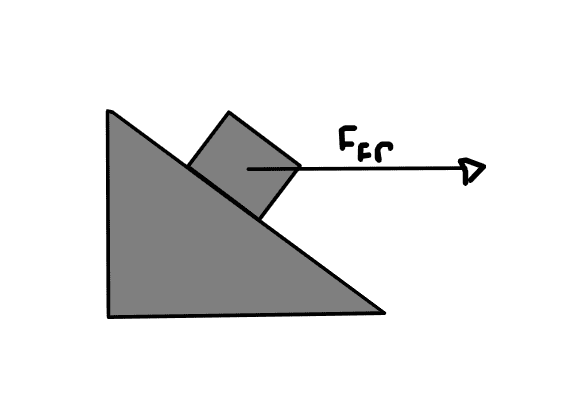
OR

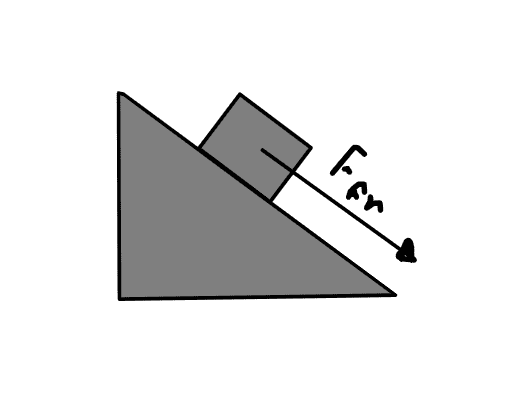
Thanks in advance for the help!

 

[BvU]

Hello R²,

!​

... curve of radius 72m banked at an angle of 14°

Cos(40°)

Why 40° ? Do you know how steep that is !

I figured out the angle by using certain geometrical properties.

That doesn't help us help you. Post what you did !

F = 1050 * (23.6^2/72) = 8122 N
(I found 23.6 by dividing 85000 by 3600)

Do not round off to three digits and then write down four digits. F is 8130 N.
Best is to work with synbols to the very end and only then round off sensibly after the calculation.

Will the frictional force of the car point directly to the center of the circular motion or will it point down towards the direction of the ramp?

Which way is it when the car stands still on the ramp ?

 

[RoboRaptor]

Hey BvU!

Why 40° ? Do you know how steep that is !

I just realized how I wrote 40° instead of 14°, that was just a silly mistake on my part . However, this changes the other 50° angle to 76°.

That doesn't help us help you. Post what you did !

Here's a more detailed image of my work. It's a bit messy but I hope you can understand it.

Which way is it when the car stands still on the ramp ?

Not sure I understand the question. Basically, I want to know in which way the frictional force is going to be directed while the car is on the ramp moving in a uniform circular motion, if I'm not wrong the object is static if looked at from reference to the circle.
and thanks for the reply!

 

[haruspex]

First I figured out the normal force being exerted on the car using the equation above.
Cos(40°)*(1050*9.8) = 7883N

That is the component of the gravitational force in the direction normal to the road. It is not necessarily the same as the normal force from the road.

Your diagram sure is messy. Just show the car and the forces on it. What are they, and in what directions do they act?
Their resultant produces the acceleration. What are the magnitude and direction of that?
What two equations does that allow you to write?

 

[RoboRaptor]

That is the component of the gravitational force in the direction normal to the road. It is not necessarily the same as the normal force from the road.

I assumed that was the case because I thought Normal Force had the same magnitude as the force that is being applied perpendicular to the road, in this case, the y-component of the weight.
Our teacher taught us a way to do free-body diagrams on inclined ramps which I'm not sure if it's the norm for this type of problems, here it is:

 

[haruspex]

I assumed that was the case because I thought Normal Force had the same magnitude as the force that is being applied perpendicular to the road, in this case, the y-component of the weight.

That is only true if there is no acceleration component in that direction. You will find through this problem that there is such.

View attachment 279053

You can't just invent a mysterious force exerted by the car. There may be a frictional force in that position and orientation, so let’s agree it is that, but, again, you cannot just assume it is equal to another force. You have to justify such an equality by means of Newton's law ΣF=ma.
The diagram is good; it shows all the applied forces.
What is the resultant force, given the motion of the car?
What equations can you write for the forces?

 

[kuruman]

The diagram is good; it shows all the applied forces.

The diagram may show all the forces, nevertheless it is confusing for it uses two separate Cartesian axes simultaneously. For example, the x-component of the normal force, F_nx is shown horizontal whilst the x-component of the weight, F_wx is shown along the incline. Which is it?

 

[haruspex]

The diagram may show all the forces, nevertheless it is confusing for it uses two separate Cartesian axes simultaneously. For example, the x-component of the normal force, F_nx is shown horizontal whilst the x-component of the weight, F_wx is shown along the incline. Which is it?

Yes, good catch. I hadn't paid attention to F_wx and F_wy.