SUMMARY
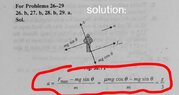
This discussion clarifies the relationship between static friction and gravitational forces on a conveyor belt. It establishes that static friction can exceed the component of gravitational force when the conveyor belt is accelerating. The confusion arises from a misunderstanding of Newton's third law and the maximum static friction coefficient, μs, which can vary between material pairs. The conversation concludes with a consensus on the principles of static friction and its application in physics.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with static friction and its coefficient (μs)
- Basic knowledge of forces acting on objects in motion
- Concept of acceleration and its effects on friction
NEXT STEPS
- Study the principles of Newton's laws in-depth
- Learn about the coefficient of friction for various material pairs
- Explore the dynamics of objects on inclined planes
- Investigate real-world applications of static friction in machinery
USEFUL FOR
Students of physics, educators teaching mechanics, and anyone interested in understanding the dynamics of friction and motion on conveyor systems.