A Parabola and Ellipse question.

[ultimatejester]

Hi everyone.

I tried solving these questions but can't seems to get anywhere. I am not used to questions like these specially word problems. Sorry if this is the wrong section.

Question 1:
The receiver of the satellite dish is at the focus of the parabola dish. The focus is 80 cm from the vertex of the dish. If the dish is 4m in diameter, find it depth.

Question 2:
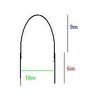
The ceiling in a hallway 10m wide is in the shape of a semiellipse. The semiellipse is 9m high in the centre. The walls of the hallway are 6m high. Find the height of the ceiling 2 m from either wall.

I could even draw the diagram for the second one.


Thnx for the help.

 

[AKG]

Question 1:
The receiver of the satellite dish is at the focus of the parabola dish. The focus is 80 cm from the vertex of the dish. If the dish is 4m in diameter, find it depth.

Model the dish as the parabola with equation:

y = ax^2 + 0.80

This puts the focus at (0, 1.60) and the directrix is the x-axis (a > 0). Now, you also know that any point on the parabola is equally distant from the focus and the directrix, so you can set up another equation:

y = \sqrt{(y - 1.60)^2 - x^2}

Finally, the depth will be the y-value of the parabola at its highest point minus the y-value at the lowest point. You know the lowest point is at the vertex of the parabola, where y = 0.80. Since the parabola is a dish that's 4m in diameter, the "highest point" occurs when x = 2.0 or -2.0. Hopefully, you understand why that is. So, we have another equation:

x = 2.0

Now, you have 3 equations, 3 unknowns, I'll leave the solution to you. Simply solve for y and do the necessary subtraction to find the depth of the dish.

Question 2:
The ceiling in a hallway 10m wide is in the shape of a semiellipse. The semiellipse is 9m high in the centre. The walls of the hallway are 6m high. Find the height of the ceiling 2 m from either wall.

Okay, this is how to visualize it: you have a hallway that is essentially 9 + 6 = 15m high. From the bottom, the walls go straight up for 6m, then start curving inwards and meet each other at the top of the ceiling. I'll let you try it on your own first, I've attached an image for you to help with the visualization.

 

[Chen]

AKG, are you sure when they say "[t]he semiellipse is 9m high in the centre" it means that it is 9 meters high above the walls? I thought it means that the center of the semiellipse is 9 meters above the ground, making it 3 meters above the walls, with a total height of the hallway being 9m.

 

[ultimatejester]

AKG, are you sure when they say "[t]he semiellipse is 9m high in the centre" it means that it is 9 meters high above the walls? I thought it means that the center of the semiellipse is 9 meters above the ground, making it 3 meters above the walls, with a total height of the hallway being 9m.

Thts, exactly what i was thinking.

 

[AKG]

Well, it says that the ceiling is in the shape of a semi-elipse and that semi-elipse is 9m high. If it were like what you (Chen and ultimatejester) were thinking, then I believe they would have said that the halway was in the shape of the semi-elipse, which was 9m high. I'm not entirely sure, though; it's a poorly-worded question. I would pick one way, and go with it, or if it matters and you want to be safe, do it both ways.