AB=AC,∠ABD=60°,∠ADB=70°,∠BDC=40°,find∠DBC

  • Context: MHB 
  • Thread starter Thread starter Albert1
  • Start date Start date
Click For Summary
SUMMARY

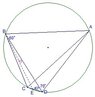
The discussion focuses on solving for the angle ∠DBC in quadrilateral ABCD, where sides AB and AC are equal, specifically given the angles ∠ABD = 60°, ∠ADB = 70°, and ∠BDC = 40°. Using the properties of isosceles triangles and the sum of angles in a triangle, the solution concludes that ∠DBC equals 50°. This conclusion is derived through geometric reasoning and angle relationships within the quadrilateral.

PREREQUISITES
  • Understanding of basic geometric principles, particularly triangle properties.
  • Knowledge of angle relationships in quadrilaterals.
  • Familiarity with isosceles triangle properties.
  • Ability to apply the sum of angles theorem in triangles.
NEXT STEPS
  • Study the properties of isosceles triangles in depth.
  • Learn about the sum of angles in polygons, focusing on quadrilaterals.
  • Explore geometric proofs involving angle calculations.
  • Practice solving for unknown angles in various geometric shapes.
USEFUL FOR

Students studying geometry, educators teaching angle relationships, and anyone interested in solving geometric problems involving quadrilaterals.

Albert1
Messages
1,221
Reaction score
0
$Quadrilateral \,\,ABCD,\overline{AB}=\overline{AC} ,\angle ABD=60^o,\angle ADB=70^o,
\angle BDC=40^o,find \,\, \angle DBC=?$
 
Last edited:
Mathematics news on Phys.org
Albert said:
$Quadrilateral \,\,ABCD,\overline{AB}=\overline{AC} ,\angle ABD=60^o,\angle ADB=70^o,
\angle BDC=40^o,find \,\, \angle DBC=?$
hint:
using the diagram:
construct a point E between $\overline{CD},and \,\, \angle ABE=70 ^o$
prove points C and E overlap
View attachment 6993
 

Attachments

  • Angle DBC.jpg
    Angle DBC.jpg
    8.5 KB · Views: 114
from previous diagram we have:
Points $A,B,E,D$ cocyclic, so $\overset{\frown}{AB}=\overset{\frown}{AE}=140^o$
we get $\overline{AB}=\overline{AE}=\overline{AC}$
and points C and E overlap (since points C,E,D colinear)
$\therefore \angle DBC=\angle DBE=10^o$
 

Similar threads

MHB Geometry Challenge: Prove $\angle ADE=\angle BDC$ in Convex Quadrilateral $ADBE$
  • · Replies 3 ·
Replies
3
Views
1K
MHB How to Find the Area of Quadrilateral ABCD with Given Side Lengths and Angles?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Can AC^2 be Proven to Equal AB(AB+BC) in Triangle ABC with Angles B=80 and C=40?
  • · Replies 3 ·
Replies
3
Views
2K
MHB Calculate $\angle ADC$ in a Convex Quadrilateral
  • · Replies 5 ·
Replies
5
Views
2K
MHB Simplify a+b+c+d+2(ab+ac+ad+bc+bd+cd)+4(abc+abd+acd+bcd)+8(abcd)
  • · Replies 3 ·
Replies
3
Views
3K
MHB What Is $\angle ADB$ in a Plane with Given Side Lengths?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Geometry Challenge: Find $\angle BCD$ in Convex Quadrilateral
  • · Replies 10 ·
Replies
10
Views
3K
MHB Parallelogram ABCD: Finding AC from PB & PD
  • · Replies 1 ·
Replies
1
Views
1K
MHB Could you help me set up these geometric problems?
  • · Replies 2 ·
Replies
2
Views
3K
MHB Finding $\angle ADC$ in $\triangle ABC$
  • · Replies 3 ·
Replies
3
Views
2K