daraphy
- 13
- 2
- TL;DR
- Lift Equation gives me 12.25 Newtons per wing. Am I using it right?
Saw this equation on Nasa's website about lift equation:
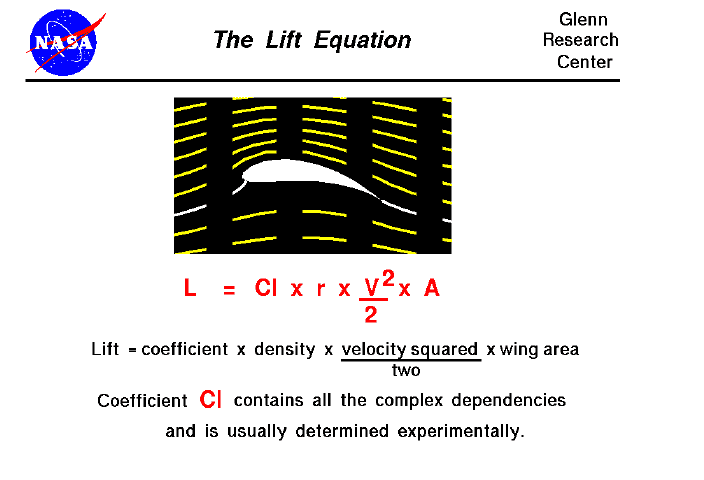
I'm trying to build a miniature helicopter and decided to test that equation.
For CI I used 0.5 because I saw a graph where flat air foils gets 0.5 CI when placed at around 10 degrees.
For air density I went with 1.225 because I live near sea levels.
For Velocity I used 20m/s and for A I used 0.1 m^2.
0.5 * 1.225 * (20^2)/2 * 0.1 = 12.25 N (I'm guessing the output is in newtons)
If multiplied by 4 wings, it gives 49N. Divided by gravity, around 5Kg.
Am I doing this right? Does that mean 3 0.1m^2 wings can lift around 5Kg?
I'm trying to build a miniature helicopter and decided to test that equation.
For CI I used 0.5 because I saw a graph where flat air foils gets 0.5 CI when placed at around 10 degrees.
For air density I went with 1.225 because I live near sea levels.
For Velocity I used 20m/s and for A I used 0.1 m^2.
0.5 * 1.225 * (20^2)/2 * 0.1 = 12.25 N (I'm guessing the output is in newtons)
If multiplied by 4 wings, it gives 49N. Divided by gravity, around 5Kg.
Am I doing this right? Does that mean 3 0.1m^2 wings can lift around 5Kg?