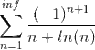SUMMARY
The discussion focuses on the absolute convergence of the series defined by the summation ##\sum_{n = 1}^\infty \frac{(-1)^{n + 1}}{n + \ln(n)}##. The limit comparison test is utilized to analyze the series, concluding that since the harmonic series diverges, the series in question also diverges. Participants emphasize the importance of using proper LaTeX formatting for clarity in mathematical expressions.
PREREQUISITES
- Understanding of series convergence concepts
- Familiarity with the limit comparison test
- Knowledge of harmonic series properties
- Basic proficiency in LaTeX for mathematical notation
NEXT STEPS
- Study the properties of the harmonic series in detail
- Learn about the limit comparison test and its applications
- Explore other convergence tests such as the ratio test and root test
- Practice using LaTeX for mathematical expressions and formatting
USEFUL FOR
Students studying calculus, mathematicians analyzing series convergence, and educators teaching mathematical notation and convergence tests.