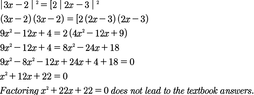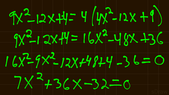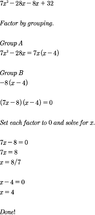Absolute Value Equation |3x - 2|/|2x - 3| = 2

Click For Summary

Discussion Overview

The discussion revolves around solving the absolute value equation |3x - 2|/|2x - 3| = 2. Participants explore different methods for finding solutions, including algebraic manipulation and squaring both sides of the equation. The conversation includes attempts to reconcile differing results with textbook answers.

Discussion Character

  • Exploratory, Technical explanation, Debate/contested, Mathematical reasoning

Main Points Raised

  • One participant presents an initial solution leading to x = 4 but notes the existence of another solution, 8/7, as indicated in the textbook.
  • Another participant emphasizes the importance of not dropping absolute value signs without considering both cases, leading to the equation 3x - 2 = -2(2x - 3) as a necessary step.
  • There is a discussion about squaring both sides of the equation, with a participant questioning whether the constant 2 must also be squared, prompting clarification on the need to square it.
  • Some participants point out errors in the algebraic manipulation, particularly regarding the squaring of terms and the resulting quadratic equations.
  • A later reply suggests that the final quadratic equation derived does not factor, which raises concerns about reaching the textbook solutions.
  • Another participant mentions a sign error in the quadratic equation that was formed, indicating that the algebraic process is still under scrutiny.

Areas of Agreement / Disagreement

Participants express differing views on the correct approach to solving the equation, particularly regarding the treatment of absolute values and the squaring process. There is no consensus on the final solutions or the correctness of the derived equations.

Contextual Notes

Some participants note unresolved mathematical steps and errors in sign or squaring, which may affect the outcomes. The discussion reflects a variety of approaches and interpretations of the problem.

Who May Find This Useful

Readers interested in algebraic methods for solving absolute value equations, as well as those looking to understand common pitfalls in manipulating such equations.

mathdad
Messages
1,280
Reaction score
0
Solve the absolute value equation.

|3x - 2|/|2x - 3| = 2

Solution:

|3x - 2| = 2|2x - 3|

3x - 2 = 2(2x - 3)

3x - 2 = 4x - 6

Solving for x, I get x = 4.

However, the textbook has two answers for this problem.
The answer is also 8/7.

How do I find 8/7?
 
Mathematics news on Phys.org
RTCNTC said:
…

Solution:

|3x - 2| = 2|2x - 3|

3x - 2 = 2(2x - 3)

…
As MarkFL pointed out in https://mathhelpboards.com/pre-algebra-algebra-2/absolute-value-equation-1-a-25152.html, you can’t just drop the absolute-value signs just like that! Otherwise you could have
$$|1|=|-1|\ \implies\ 1=-1.$$
The other solution you missed was
$$3x-2\ =\ -2(2x-3).$$
Alternatively, you can also do what you did in https://mathhelpboards.com/pre-algebra-algebra-2/absolute-value-equation-2-a-25153.html: square both sides.
 
3x−2 = −2(2x−3)

3x - 2 = -4x + 6

3x + 4x = 6 + 2

7x = 8

x = 8/7

- - - Updated - - -

Olinguito said:
As MarkFL pointed out in https://mathhelpboards.com/pre-algebra-algebra-2/absolute-value-equation-1-a-25152.html, you can’t just drop the absolute-value signs just like that! Otherwise you could have
$$|1|=|-1|\ \implies\ 1=-1.$$
The other solution you missed was
$$3x-2\ =\ -2(2x-3).$$
Alternatively, you can also do what you did in https://mathhelpboards.com/pre-algebra-algebra-2/absolute-value-equation-2-a-25153.html: square both sides.


If I decide to square both sides, must I also square 2?

Like this:

|3x - 2|^2 = [2|2x - 3|]^2

or

Like this:

|3x - 2|^2 = 2[|2x - 3|]^2
 
RTCNTC said:
3x−2 = −2(2x−3)

3x - 2 = -4x + 6

3x + 4x = 6 + 2

7x = 8

x = 8/7

- - - Updated - - -
If I decide to square both sides, must I also square 2?

Like this:

|3x - 2|^2 = [2|2x - 3|]^2

or

Like this:

|3x - 2|^2 = 2[|2x - 3|]^2
Yes, you have to square the 2 as well. [math](a (x - 1))^2 = a^2 (x - 1)^2[/math] for example.

-Dan
 
topsquark said:
Yes, you have to square the 2 as well. [math](a (x - 1))^2 = a^2 (x - 1)^2[/math] for example.

-Dan

It really helps to know that 2 must also be squared.
 
Take a look at my reply. The final quadratic equation does not factor leading to the textbook answers.

View attachment 8536
 

Attachments

  • MathMagic181029_1.png
    MathMagic181029_1.png
    18.1 KB · Views: 154
You didn't square the 2 on the RHS.
 
MarkFL said:
You didn't square the 2 on the RHS.

You are right.
 
I squared 2 on the right side but ended up with a quadratic equation that does not lead to the textbook answers. See picture.

View attachment 8537
 

Attachments

  • sDraw_2018-10-29_11-15-56.png
    sDraw_2018-10-29_11-15-56.png
    30.8 KB · Views: 131
  • #10
You've made a sign error, you should get:

$$7x^2-36x+32=0$$
 
  • #11

Attachments

  • MathMagic181029_1.png
    MathMagic181029_1.png
    18.1 KB · Views: 135

Similar threads

MHB Solve Absolute Value Equation |(2x + 1)|/|(3x + 4)| = 1
  • · Replies 4 ·
Replies
4
Views
1K
MHB Equation 2: Prove that ##x^2+2x\sqrt x+3x+2\sqrt x+1=0##
  • · Replies 4 ·
Replies
4
Views
2K
MHB Quadratic equations ( solving for zeros/roots) trickey
  • · Replies 1 ·
Replies
1
Views
1K
MHB Solve Inequality & Simul Eqns: Alg Workings Q (a,b,c)
  • · Replies 1 ·
Replies
1
Views
1K
MHB Find Polynomial Given Remainder After Division
  • · Replies 6 ·
Replies
6
Views
2K
MHB Solve Absolute Value Equation |x^2 - 2x| = |x^2 + 6x|
  • · Replies 6 ·
Replies
6
Views
2K
MHB Solve √(x^2+3x+7)-√(x^2-3x+9)+2=0
  • · Replies 5 ·
Replies
5
Views
2K
MHB Real Roots of Cubic Equation: $x^3+a^3x^2+b^3x+c^3=0$
  • · Replies 1 ·
Replies
1
Views
2K
How Do You Solve Complex Absolute Value Inequalities?
  • · Replies 4 ·
Replies
4
Views
2K
MHB Which procedure takes the minimum time to solve modulus functions?
  • · Replies 5 ·
Replies
5
Views
1K