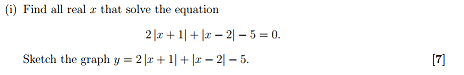To solve the absolute value problem, the expression is defined as a piecewise function with three segments. The only solution found so far is at x=1, but there should be two valid roots within the specified domains. To sketch the area between -1 and 2, calculate the endpoints of the middle segment, which are f(-1) = -2 and f(2) = 1. Plot the points (-1, -2) and (2, 1), then connect them with a line segment to complete the graph. Understanding the roots and their respective domains is crucial for accurate representation.