SUMMARY
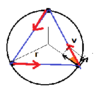
The discussion centers on the initial acceleration of three particles A, B, and C, positioned at the vertices of an equilateral triangle of side length l, as they move toward each other with a constant velocity v. The participants analyze the relationship between velocity and acceleration, concluding that while the magnitude of velocity remains constant, the direction changes, leading to a non-zero initial acceleration. The acceleration is derived using the formula a = (3v/2)(dθ/dt), where dθ/dt represents the rate of change of the direction of the velocity vector. The conversation emphasizes the importance of understanding the dynamics of motion in a triangular formation.
PREREQUISITES
- Understanding of vector components in physics
- Familiarity with uniform circular motion concepts
- Knowledge of polar coordinates and their applications in dynamics
- Ability to differentiate trigonometric functions
NEXT STEPS
- Study the derivation of acceleration in uniform circular motion
- Explore the application of polar coordinates in dynamic systems
- Learn about the relationship between angular velocity and linear velocity
- Investigate the mathematical modeling of particle motion in triangular formations
USEFUL FOR
Students of physics, particularly those studying dynamics, mathematicians interested in motion analysis, and educators seeking to explain complex motion scenarios involving multiple particles.