- #1
Satvik Pandey
- 591
- 12
Homework Statement
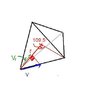
4 ants are arranged in such a way that they make up vertex of a regular tetrahedron, of side length 1m . The ants are named Calvin , Peter , David and Aron. Each ant moves at a speed 1m/s , and moves in such a way that:
Calvin moves toward Peter,
Peter moves toward David,
David moves toward Arron,
Arron moves toward Calvin
If they continue to moves it this direction they will converge somewhere. What time in seconds will it take the ants to meet each other?
Homework Equations
The Attempt at a Solution
The base of tetrahedron will form an equilateral triangle.
Length of side of equilateral triangle(a)=2cos 35.5
It is given Peter moves toward David, David moves toward Arron.
V[itex]_{PD}[/itex](relative velocity of Peter w.r.t.Arron) =√3V
Projection of V[itex]_{PD}[/itex] on line of motion of Peter=√3Vcos30[itex]^{°}[/itex]=[itex]\frac{3V}{2}[/itex]
now
∫[itex]^{0}_{a}[/itex]dl=∫[itex]^{t}_{0}[/itex][itex]\frac{3V}{2}[/itex]
t=2a/3V
=4*cos(35.5)/3
But this is not correct.
Last edited: