Adjoint of Schrodinger Equation

[catsarebad]

I'm missing something obvious so please point out what I'm thinking wrong

SE equation is:

ih d/dt |

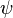> = H|

>

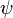the taking adjoint turns i -> -i and (d/dt) -> -(d/dt)

so adjoint of SE should be same as SE

however it isn't. adjoint of SE is

-ih d/dt |

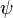> = H|

>

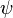do we not take adjoint of d/dt, if so, why not? the adjoint of d/dt is -d/dt, no?

thanks a bunch in advance.

 

[bhobba]

Its a bit tricky because the time evolution operator T has a negative sign in it ie is e^(-iHt) (in units h bar =1 for simplicity) . That way you get a minus sign when you take the derivative.

The reason has to do with the sign that appears when you look at them as generators and you can find the gory detail in Chapter 3 of Ballentine:
https://www.amazon.com/dp/9810241054/?tag=pfamazon01-20

In particular have a look at page 77 where the velocity operator is introduced in equation 3.37. Chug through the math and you end up with the form of the time evolution operator with the negative sign which leads to Schroedinger's equation - equation 3.38.

Thanks
Bill

 

[dextercioby]

d/dt is not a true operator, so you can' talk about its adjoint (provided it exists).

 

[catsarebad]

d/dt is not a true operator, so you can' talk about its adjoint (provided it exists).

elaborate please. why is this not a true operator?

I know adjoint of d/dx is -d/dx. i found it on net and book.

 

[bhobba]

elaborate please. why is this not a true operator?

States are generally considered to reside in a Hilbert space, which are Lebesgue square integrable functions. Such functions are not always differentiable so the differentiation operator does not exist for all elements of the space.

There are ways around it, using what are Rigged Hilbert Spaces is probably the most common.

Thanks
Bill

 

[stevendaryl]

States are generally considered to reside in a Hilbert space, which are Lebesgue square integrable functions. Such functions are not always differentiable so the differentiation operator does not exist for all elements of the space.

There are ways around it, using what are Rigged Hilbert Spaces is probably the most common.

Thanks
Bill

Hmm, I feel like the reason that \frac{d}{dt} isn't a true operator is different from the reason that \frac{d}{dx} isn't a true operator. It's not about square-integrability.

In the usual way that non-relativistic QM is done, the Hilbert space is a space of functions of position alone. A basis is complete if you can construct any square-integrable function of position. But time is treated differently. In the treatments I've seen, there is no comparable notion of completeness with respect to functions of time.

 

[stevendaryl]

elaborate please. why is this not a true operator?

I know adjoint of d/dx is -d/dx. i found it on net and book.

When people are talking about "adjoints" they are talking about operators on the Hilbert space. The Hilbert space is a space of functions of position, not position and time. So \frac{d}{dt} is not an operator on the Hilbert space. It is certainly a meaningful operator on functions on spacetime, but it isn't a meaningful operator on functions of space, which is what the elements of the Hilbert space are.