I Algebra equation with variable as exponent

[adamaero]

This equation takes a present value (PV) to find mortgage payments, PMT:

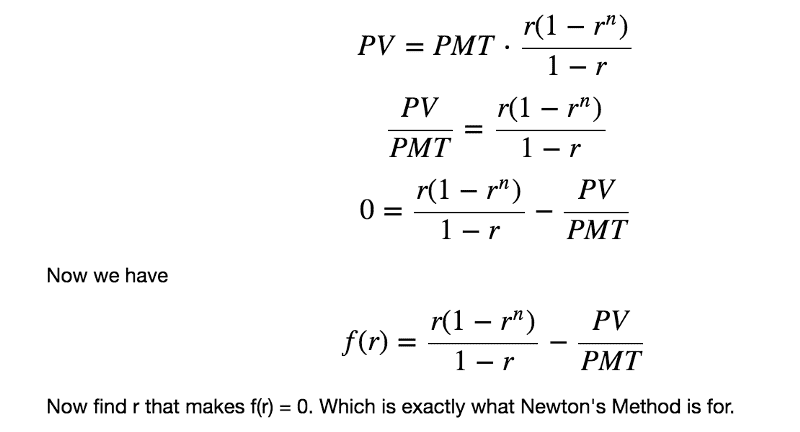
Alternatively, switching V for PV and T for PMT:
V/T = r(1-r^n)/(1-r)

What is an algebraic method to solve for "r"?
Can it not be solved for? I realize I can just find out "r" by trial by error in Excel using the PMT function.

Although, I would like to find a way to just solve for "r" outright. Thanks.

 

[anuttarasammyak]

I do not think there is an algebraic method for. As text says computtion by Newton's method https://en.wikipedia.org/wiki/Newton's_method seems applicable.

 

[adamaero]

I

As text says computtion by Newton's method https://en.wikipedia.org/wiki/Newton's_method seems applicable.

It is just a random picture. Newton's method can be punched into an excel spreadsheet?

How?

 

[anuttarasammyak]

Alternatively, switching V for PV and T for PMT:
V/T = r(1-r^n)/(1-r)

Let me write it in order to use ordinary x-y graph picture
y=f(x)=\frac{x(1-x^n)}{1-x}-a
where n is not a variable but a given number and
a=\frac{PV}{PMT}
is also a given number. The problem is to find x where y=0.

The prescription of Newton method :

Preparation
1 . Get formula of derivative f'(x)
2 . Get formula of tangential line at (x,y=f(x)) with 1.
3 . Get formula of x where the tangential line cross with x-axis with 2, say g(x).

Then
Let x=$x_0$ which you assume to be approximate solution
Get value of $x_1=g(x_0)$
Get value of $x_2=g(x_1)$
Get value of $x_3=g(x_2)$
----

Repeat it until you find $x_n$ seem to remain unchanged in PC calcualtion that means $f(x_n)$ is enough close to zero in your calculation environment.

 

[pasmith]

I suspect that you are looking for the Excel RATE function, which is described as follows:

Description

Returns the interest rate per period of an annuity. RATE is calculated by iteration and can have zero or more solutions. If the successive results of RATE do not converge to within 0.0000001 after 20 iterations, RATE returns the #NUM! error value.

Syntax

RATE(nper, pmt, pv, [fv], [type], [guess])

 

[adamaero]

I suspect that you are looking for the Excel RATE function, which is described as follows:

Thank you!

 

[BWV]

THe formula in the OP does not look right. for n=1 and r=.05 it gives a discount factor of (.05)(.95)/.95 = .05 the correct factor is (1+r)^-1=.95

The discount factor of a payment in perpetuity is simply

r^-1

A finite series of payments is simply the sum of each payment's PV, so the PV of a stream of $1 payments is

Σ(1+r)^-n with n going from first to last payment

 

[BWV]

you can also get rid of the exponents by switching to log returns and continuous compounding

so
(1+r)^-n = exp[-rn] where r = log(1+r)