Kevin Licer
- 21
- 0
Member warned about posting with no template
So I stumbled upon this problem:
Solve:
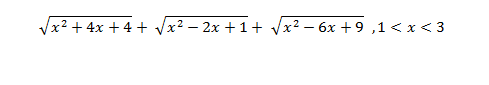
And I have attempted to solve it, however my solution doesn't match that of the book.
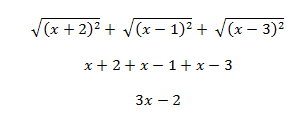
The solution should be x+4, but I don't have a clue how to get to that. I'm sorry if this seems pretty rudimentary, but I just want some help because it's the first time I've dealt with an equation like this (1<x<3 what should I do with that?). Any help is appreciated. Thanks!
Solve:
And I have attempted to solve it, however my solution doesn't match that of the book.
The solution should be x+4, but I don't have a clue how to get to that. I'm sorry if this seems pretty rudimentary, but I just want some help because it's the first time I've dealt with an equation like this (1<x<3 what should I do with that?). Any help is appreciated. Thanks!