- #1
brotherbobby
- 625
- 155
- Homework Statement
- At what values of ##a## does the equation ##2x^2-(a^3+8a-1)x+a^2-4a = 0## possess roots of opposite signs?
- Relevant Equations
- For a quadratic equation ##ax^2+bx+c=0## having roots ##\alpha,\beta##, the sum of the roots ##\alpha+\beta = -\frac{b}{a}## and product of the roots ##\alpha\beta = \frac{c}{a}##.
Given : The equation ##2x^2-(a^3+8a-1)x+a^2-4a = 0## with roots of opposite signs.
Required : What is the value of ##a## ?
Attempt : The roots of the equation must be of the form ##\alpha, -\alpha##. The sum of the roots ##0 = a^3+8a-1##.
I do not know how to solve this equation.
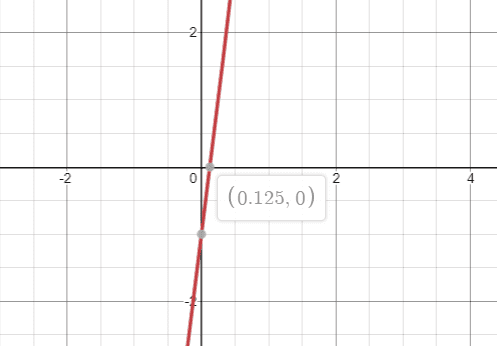 However, on plotting the graph of this function [##f(x) = x^3+8x-1##], I find that ##a = 0.125##.
However, on plotting the graph of this function [##f(x) = x^3+8x-1##], I find that ##a = 0.125##.
However, this is not the answer in the book.
Answer : ##a \in (0;4)## (from book)
Any help would be welcome.
Required : What is the value of ##a## ?
Attempt : The roots of the equation must be of the form ##\alpha, -\alpha##. The sum of the roots ##0 = a^3+8a-1##.
I do not know how to solve this equation.
However, this is not the answer in the book.
Answer : ##a \in (0;4)## (from book)
Any help would be welcome.