SUMMARY
The discussion centers on the dynamics of an object with mass m moving along the x-axis, governed by the potential energy function Ep(x) = (1/2)*k*(x^2 - 4)^2. Participants confirm the correctness of calculations related to the system's energy and velocity, specifically addressing the conditions under which v=0 and the total energy required to reach x=0. The total energy needed for this system is established as 9/2 k, and there is a focus on the accuracy of the graphical representation of the potential energy curve.
PREREQUISITES
- Understanding of classical mechanics principles, particularly energy conservation.
- Familiarity with potential energy functions and their graphical representations.
- Knowledge of calculus, specifically derivatives and their application in motion analysis.
- Experience with solving quadratic equations related to motion dynamics.
NEXT STEPS
- Investigate the implications of potential energy functions in mechanical systems.
- Learn about energy conservation in conservative force fields.
- Explore the relationship between potential energy and kinetic energy in oscillatory motion.
- Study the graphical interpretation of energy curves and their physical significance.
USEFUL FOR
Students and professionals in physics, particularly those studying mechanics, as well as engineers and researchers involved in dynamic systems analysis.

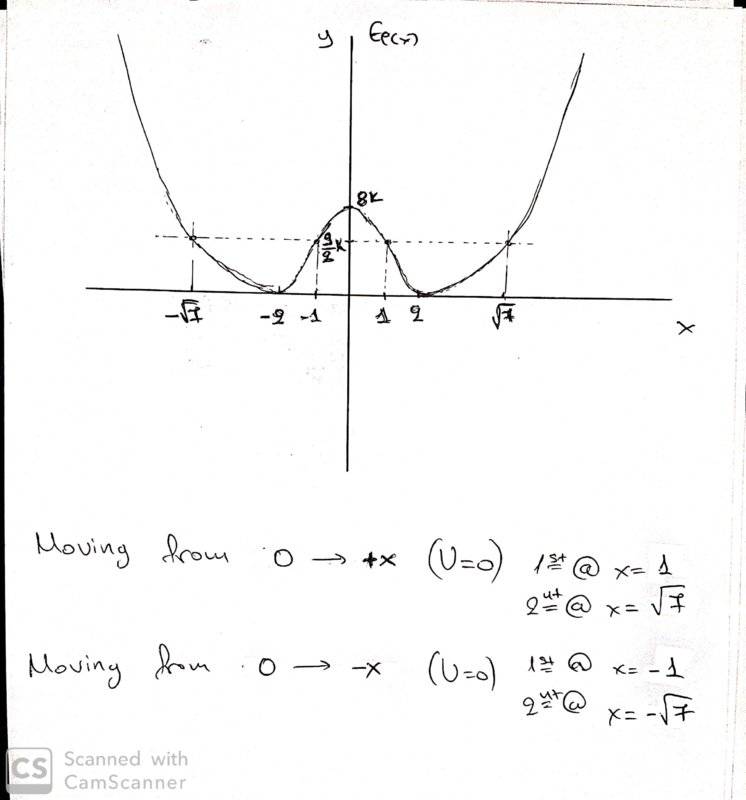 Is that correct ?
Is that correct ?