A planet of mass M and an object of mass m

[Angela G]

Homework Statement

HI! I wonder if you could please help me with this excercise. It is from a course about planets.

A planet of mass M and radius R initially an angular velocity of w and no obliquity. It is impacted nearly tangentially at its north pole by a body of mass m≪ M, whose relative velocity before the encounter is small compared to the escape speed from the planet’s surface

Derive an expression for the planet’s angular velocity and obliquity after the impact in terms of M, m,R, $\omega$,

Relevant Equations

$$ I = \frac{2}{5}MR^2$$
$$ L = r x p$$
$$ L = Iw $$

HI!
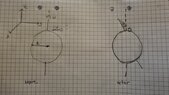
I tried to solve this exercise, by assuming that it is an inelastic collision, the planet is spherical, and that the rotation axis is parallel to the z-axis, see the figure attached. (1) before the collision, (2) after the collision.I started by assuming angular momentum conservation, which means that $L_i = L_f$ where 'i' refers to the initial and 'f' is the final.

The initial angular momentum $L_i = L_o +L_p$ ( is the sum of the angular momentum of the object and the planet). The angular momentum of the planet is given by $L_p = I * \omega$ where $\omega$ is the angular velocity before the collision, and $I$ is the moment of inertia $I = \frac{2}{5} M*R^2$ . The angular momentum of the object is given by $L_o = r \times p = r sin(\theta)mv$. For the initial values, we set that $\theta = 90$ since the object hits the planet tangentially. So we have that $L_o = Rmv$. For the final angular momentum, we have that $L_f = I' \omega '$. We equate both side and get

$$ \frac{2}{5} M*R^2 * \omega + Rmv = I' \omega ' \Longrightarrow \frac{2}{5} M*R^2 * \omega + Rmv = \frac{2}{5}(M+m)R^2 \omega ' $$
we solve for $\omega '$ and we get
$$ \frac{5}{2(M+m)R^2}\left(\frac{2}{5} M*R^2 * \omega + Rmv \right)= \omega ' $$

But the problem is that I have still a term with the velocity of the object, which I should not get. I wonder if someone can please help me with this and if I can also solve this with forces.

Best regards
Angela

 

[nasu]

What axis (or point) do you use when you calculate the angular momentum of the small mass before the collision?

 

[Angela G]

r is in the same direction as the radius of the planet(out from the centrum), and p is in the direction of the velocity, if we assume that the object is going to the planet from right to left as in the picture, then the momentum is in the negative y-axis. my reference frame is: the z-axis is positive at the pole (upwards), y-axis defined positive at the right, and the x-axis defined as positive out from the plane.

 

[kuruman]

The problem is unclear about the velocity of the smaller mass. Yes, the collision occurs at the planet's north pole but that is not enough. If we take the "12 o' clock" position to be the direction of the planet's orbital velocity, at what "o' clock" position is the direction of the velocity of the smaller mass at the time of the collision? Maybe that is variable that figures in the solution.

Also, I think that the given angular velocity $\omega$ is the orbital angular velocity of the planet not the spin angular velocity. If it were the spin, we would still need to know the initial orbital angular momentum.

 

[nasu]

r is in the same direction as the radius of the planet(out from the centrum), and p is in the direction of the velocity, if we assume that the object is going to the planet from right to left as in the picture, then the momentum is in the negative y-axis. my reference frame is: the z-axis is positive at the pole (upwards), y-axis defined positive at the right, and the x-axis defined as positive out from the plane.

You add the spin angular momentum of the planet around it's polar axis with the angular momentum of the small object around the center. They are not in the same direction, are they? But before even adding or using equations you need to clarify what is actually going on.

 

[Angela G]

Sorry for being unclear,
I have a planet that has a spin angular velocity $\omega$, its rotation axis is in the z-direction. The planet is impacted nearly tangentially i.e the velocity of the object just before the impact, can be assumed to be nearly tangential, thus we chose the negative y-direction (at 9 o'clock). Since it is an inelastic collision, the object is absorbed. Also, just before the collision, the velocity of the object is smaller than the escape velocity of the planet.

The question is to derive an equation for the new spin angular velocity of the planet after the impact. this collision also changed the obliquity of the planet, that's the second question: to derive the obliquityAttached is a possibly better picture

 

[nasu]

If you apply a force along the y axis the polar axis should tilt in the x direction. The torque of the impact force (which acts along the y axis in your diagram) relative to the cenetr is along the x axis so the change in the angular momentum has to be in this direction.