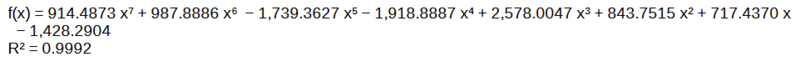- 2,180
- 2,694
We recently did an experiment to generate the hysteresis curve of a certain material. The experiment involved switching the current in the wire looped around a ring of the material, and recording the first throw of the ballistic galvanometer. I am not going into the details of calculations because the thread is intended to be regarding curve fitting. After certain calculations, we arrived at the following data for a graph of B vs H (in MATLAB):
Note that this is only half of the hysteresis curve; the other half is to be plotted by symmetry.
I am supposed to find the best fit curve for this data. Some further calculations need to be done on the area between the two curves.
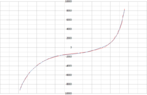
For non-linear regression, I generally use the Shape Language Modelling tool available on MATLAB File Exchange. I am creating the model as follows:
I can get different shapes of curves by choosing different values for the number of knots. The default is 6. If I increase the number of knots, the root-mean-square error (RMSE) decreases until it reaches
The curves with higher number of knots seem to be closer to the data points. However, looking at the unevenness of the curve near the bottom, I was wondering if I am overfitting the data? Should I blindly go with the RMSE and choose the curve with 70 knots, or am I indeed overfitting and should choose a knots value somewhere in the middle?
Matlab:
B = [1.389 1.374 1.345 1.331 1.316 1.302 1.287 1.273 1.258 1.229 1.215 1.215 1.172 1.128 1.114 ...
1.099 1.056 1.041 1.027 1.013 0.984 0.969 0.969 0.955 0.839 0.448 0.391 0.275 0.130 -0.275 ...
-0.405 -0.579 -0.665 -0.781 -0.839 -0.882 -0.955 -0.998 -1.114 -1.201 -1.244 -1.287 -1.345 ...
-1.403 -1.432 -1.461];
H = [8409.911 7488.684 6805.193 6181.136 5289.626 5022.173 4695.286 4249.531 3982.078 3744.342 ...
3417.455 3090.568 2644.813 2258.492 2020.756 1753.303 1426.416 1248.114 1129.246 980.661 ...
921.227 832.076 772.642 653.774 0.000 -861.793 -950.944 -1069.812 -1218.397 -1575.001 -1842.454 ...
-2228.775 -2466.511 -2823.115 -3090.568 -3328.304 -3595.757 -3952.361 -4784.437 -5438.211 ...
-6002.834 -6567.457 -7250.948 -8053.307 -8558.496 -9331.138];Note that this is only half of the hysteresis curve; the other half is to be plotted by symmetry.
I am supposed to find the best fit curve for this data. Some further calculations need to be done on the area between the two curves.
For non-linear regression, I generally use the Shape Language Modelling tool available on MATLAB File Exchange. I am creating the model as follows:
Matlab:
slm = slmengine(H, B, 'increasing', 'on', 'concaveup', 'on', 'knots', no_of_knots);concaveup is the curvature constraint — the second derivative should never be negative, while increasing is the monotonicity constraint.I can get different shapes of curves by choosing different values for the number of knots. The default is 6. If I increase the number of knots, the root-mean-square error (RMSE) decreases until it reaches
no_of_knots = 70, after which it increases and the curve becomes garbage. In the Imgur post below, I have shown the curves for different number of knots. The RMSE for each curve is also shown on the plot. The dashed blue line is the other half of the hysteresis loop, generated by a centre of inversion symmetry.
The curves with higher number of knots seem to be closer to the data points. However, looking at the unevenness of the curve near the bottom, I was wondering if I am overfitting the data? Should I blindly go with the RMSE and choose the curve with 70 knots, or am I indeed overfitting and should choose a knots value somewhere in the middle?