Apparent depth equation proving

[salivian selwyn]

Homework Statement

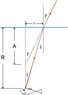
a fish at a depth d underwater.Takes the index of refraction of water as 4/3 show that when the fish is viewed at an angle of refraction θ , the apparent depth z of the fish is
z = (3d cosθ )/ √ (7 + 9 cos² θ)

Homework Equations

snell's law
n₁ x sin θ₁ = n₂ x sin θ₂

The Attempt at a Solution

(n_water) (sin θ) = (n_air) (sin r) ->[/B] since n_air is 1
(n_water) (sin θ) = sin r --- square both side
(n²_water) (sin² θ) = (sin r)
(n²) (sin² θ) = (x²) / (x² + z²)
1/((n²)(sin²θ)) = (x² + z²)/(x²)
1 + (z²/x²) = 1/((n²)(sin²θ))
z²/x² =(1-n²*sin²θ)/(n²*sin²θ)
--subtitute x with d tanθ ,give me--
z² = (d²) ((1- n²*sin²θ)/(n²*cos²θ))
using 1 = sin²θ + cos²θ identity, give me
z² = (d^2)((1+ n²*cos²θ - n²)/(n² * cos²θ))
im stuck here , this result in
z² = d²((16cos²θ - 7)/(16cos²θ))

i think it's a little bit more , but I am stuck here

 

[gleem]

Your began the wrong way first look for the relationship between R and A. Start by looking at x/R and x/a

 

[salivian selwyn]

Your began the wrong way first look for the relationship between R and A. Start by looking at x/R and x/a

Sorry ,i don't get what you mean. Can you explain it to me ?

 

[gleem]

determine the relationships between the ratios x/R and x/A to the angles i and r and then to the index of refraction..