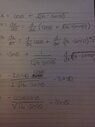SUMMARY
The discussion centers on solving a problem involving the application of differentiation to the position function \( x = \cos(\theta) + \sqrt{16 - \sin^2(\theta)} \). The user seeks assistance in finding the velocity by computing the first derivative and applying the chain rule. The derivative \( \frac{df}{\theta} = -\sin(\theta)\left(1 + \frac{\cos(\theta)}{\sqrt{16 - \sin^2(\theta)}}\right) \) has been correctly derived, but the user is unsure how to proceed with the given \( \theta = \frac{\pi}{2}t \) to find \( \frac{d\theta}{dt} \).
PREREQUISITES
- Understanding of differentiation and derivatives
- Familiarity with the chain rule in calculus
- Knowledge of trigonometric functions and their derivatives
- Ability to interpret parametric equations
NEXT STEPS
- Calculate \( \frac{d\theta}{dt} \) given \( \theta = \frac{\pi}{2}t \)
- Apply the chain rule to find the velocity function \( \frac{dx}{dt} \)
- Set the velocity function equal to zero to find critical points
- Explore applications of differentiation in physics, particularly in motion analysis
USEFUL FOR
Students and educators in calculus, particularly those focusing on applications of differentiation in physics and motion analysis.