Are the coordinates of the vertices of this triangle all integers?

[chucktingle]

L1 [x,y]=[2,1]+r[-5,1]
L2 [x,y]=[1,4]+s[2,1]
L3 [x,y]=[3,5]+t[4,-5]
These three lines are sides of a triangle
find: 1)the perimeter of the triangle
2) The largest angle
3) the centroid of the triangle

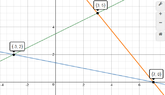
so I converted the vector equations into parametric, and then made two of the x parametric equations to equal each other to find the vertices.This gave me to vertices (-3,2), (7,0) and (3,5). The problem is the perimeter I get from those vertices is not an integer, I was told it would have no decimals. Am I going about the problem incorrectly? Once I have the vertices I can easily find the angle with cosine law, and use the centroid formula for the centroid, I am just not sure about the vertices I got.

 

[MarkFL]

I think I would convert to Cartesian coordinates:

$$L1\implies x+5y=7$$

$$L2\implies x-2y=-7$$

$$L3\implies 5x+4y=35$$

View attachment 6567

I agree with the vertices you found. And so the perimeter $P$ is:

$$P=\sqrt{6^2+3^2}+\sqrt{4^2+5^2}+\sqrt{10^2+2^2}=3\sqrt{5}+\sqrt{41}+2\sqrt{26}$$

Is this what you have?

 

[chucktingle]

I think I would convert to Cartesian coordinates:

$$L1\implies x+5y=7$$

$$L2\implies x-2y=-7$$

$$L3\implies 5x+4y=35$$
I agree with the vertices you found. And so the perimeter $P$ is:

$$P=\sqrt{6^2+3^2}+\sqrt{4^2+5^2}+\sqrt{10^2+2^2}=3\sqrt{5}+\sqrt{41}+2\sqrt{26}$$

Is this what you have?

Thanks for the reply, yep that's what I got. Maybe they rounded for the answer?

 

[MarkFL]

Thanks for the reply, yep that's what I got. Maybe they rounded for the answer?

I'm thinking that perhaps what was intended was that the coordinates of the 3 vertices would all be integers. :)