Discussion Overview
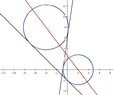
The discussion revolves around finding the standard equations of circles with centers on the line defined by the equation 4x + 3y = 8, which are also tangent to the lines x + y = -2 and 7x - y = -6. The scope includes mathematical reasoning and problem-solving related to geometry and algebra.
Discussion Character
- Mathematical reasoning
- Exploratory
- Homework-related
Main Points Raised
- One participant presents initial equations involving parameters a and b, suggesting a relationship between the center of the circle and the tangential conditions.
- Another participant questions the relevance of the parameters a and b, proposing that the center (a, b) should be defined explicitly and relates it to the line equation.
- A method is suggested to derive the conditions for tangency by forming a quadratic equation based on the circle's equation and the tangential lines.
- A later reply expresses relief upon realizing that the problem indeed allows for two possible circle centers, indicating a potential misunderstanding or concern about the uniqueness of the solution.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the approach to solving the problem, as there are differing interpretations of the initial equations and the implications of the tangency conditions. The discussion remains unresolved regarding the final formulation of the circle equations.
Contextual Notes
There are limitations in the clarity of the initial equations presented, as well as potential dependencies on the definitions of parameters used. The discussion also reflects uncertainty about the uniqueness of the solutions for the circle centers.
