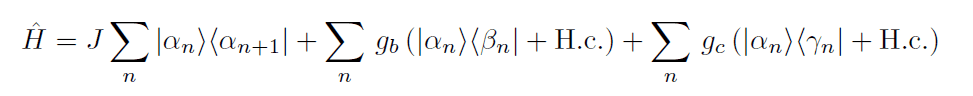Assignment on the tight binding model

[Satana]

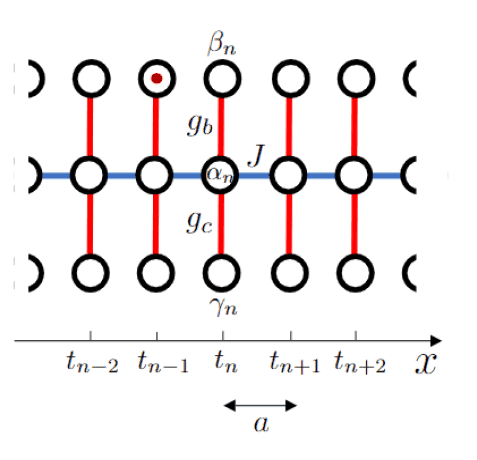
Summary:: Due tight-binding model I derived the energy spectrum of the particle, showing that it comprises three energy bands E+(k), E−(k) and E0(k)=0. Now, I have to find the dispersion laws. Why do I have a flat energy band? What is its physical significance?. Also, what happens to the particle to t→∞ if the state at t=0 is in a generic site Ψ(0)=|βm>?

 

[Satana]

$E_0(k)=0 ; E_{\pm}(k)=-Jcos(ka){\pm}\sqrt{J^2cos^2(ka)+g_c^2+g_b^2}$
These are the energy bands that I found.