I Average chord length of a circle

[serverxeon]

I would like to find the average chord length of a circle.
And I have 2 methods, which gave different answers...

[The chord is defined as the line joining 2 points on the circumference of the circle.]

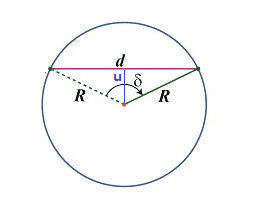
The general formula for a chord length is $d=2R\sin(\delta/2)=2\sqrt{R^2-u^2}$

Method 1: Integrate over angles
Avg length = $$\frac{\int_0^{2\pi} 2R\sin(\delta/2)\,d\delta}{2\pi}$$
$$=\frac{4R}{\pi}$$

Method 2: Integrate over diameter (-R to R)
Avg length = $$\frac{\int_{-R}^{R} 2\sqrt{R^2-u^2}\,du}{2R}$$
After simplification
$$\int_{-R}^{R} \sqrt{1-\left(\frac{u}{R}\right)^2}\,du$$
Then, using the fact
$$\int_{-Z}^{Z} \sqrt{1-\left(\frac{u}{Z}\right)^2}\,du = \frac{Z\pi}{2}$$
I get
$$=\frac{R\pi}{2}$$

So the answers from my 2 methods don't add up. Any things i might have overlooked?

 

[mfb]

You found two different definitions for the average. The question "what do you average over?" is not just interesting for the calculation, it leads to different mathematical questions - with different answers.

 

[serverxeon]

I am not too sure. Are they not the same?
However, even if I ignore the different definition of average and solely look at the 'sum of all chords',

I get (for angles) $8R$ and (for diamater) $R^2\pi$

Am I not simply summing up all possible chord lengths from 0, to 2R, then back to 0 again?

 

[mfb]

There is an infinite set of chords, there is no unique way to “sum” over them.

An analogy: Let $a=b^2$. Clearly a=b has the solutions a=b=0 and a=b=1. But the integrals between these limits are different: $$\int_0^1 a da \neq \int_0^1 b^2 db$$
The key point here is $da \neq db$ - it matters how you integrate.

 

[serverxeon]

Your example is not exactly correct.
If you substituted $$a=b^2$$
then
$$\int_0^1 a\, da = \int_0^1 {b^2\cdot2b}\,db$$
which is then the same...

Anyway,
Did you mean to say there is ONE set of infinite chords, or there are infinite sets of finite chords?
Because you seem to suggest the former, and that would mean there should only be one unique answer?

 

[mathman]

There is one set of infinite chords. However, there are many possible ways to define the probability distribution. Your analysis uses two different ones, so it is not surprising to get two different answers for the mean.

 

[mfb]

which is then the same...

Yes, but you had to introduce the factor 2 b. That's the point. A change in coordinates can change the integral if you do not add factors like these.

 

[disregardthat]

The one true way to obtain a random chord, is to uniformly pick two points P,Q on the circle. These choices amounts to a uniform choice of angles \theta,\phi \in [0,2\pi). The angle POQ, where O is the center, is equal to \sqrt{2R^2-2R^2\cos(\theta-\phi)} = \sqrt{2}R\sqrt{1-\cos(\theta - \phi)} by the cosine formula (note that the sign of \theta - \phi does not matter here). The average length thus becomes

\frac{\int^{2\pi}_0 \int^{2\pi}_0 \sqrt{2}R\sqrt{1-\cos(\theta - \phi)}d\theta d \phi}{\int^{2\pi}_0 \int^{2\pi}_0 d\theta d\phi} = \frac{\int^{2\pi}_0 \int^{2\pi}_0 \sqrt{2}R\sqrt{1-\cos(\theta - \phi)}d\theta d \phi}{(2\pi)^2}

Evaluating the inner integral first, it is clear that as \phi varies as a constant, the integral remains unaffected. So
\int^{2\pi}_0\left( \int^{2\pi}_0 \sqrt{2}R\sqrt{1-\cos(\theta - \phi)}d\theta \right) d \phi = \int^{2\pi}_0\left( \int^{2\pi}_0 \sqrt{2}R\sqrt{1-\cos(\theta)}d\theta \right) d \phi
= 2\pi \sqrt{2}R \int^{2\pi}_0 \sqrt{1-\cos(\theta)}d\theta = 2\pi \sqrt{2}R \left( \int^{\pi}_0 \sqrt{1-\cos(\theta)}d\theta + \int^{\pi}_0 \sqrt{1+\cos(\theta)}d\theta \right)

On the last equality we split the integral in two, and used the fact that \cos(\theta + \pi) = -\cos(\theta). Next observe that 1-\cos(\theta) = 2\sin^2(\frac{\theta}{2}) and 1 + \cos(\theta) = 2\sin^2(\frac{\theta}{2}), so that \sqrt{1-\cos(\theta)} = \sqrt{2}\sin(\frac{\theta}{2}) and \sqrt{1+\cos(\theta)} = \sqrt{2}\cos(\frac{\theta}{2}) (note that both expressions to the right are positive since we now are integrating over \theta \in [0,\pi]!).

Our integral becomes

2\pi \sqrt{2}R \int^{\pi}_0 \sqrt{2}\left( \sin(\frac{\theta}{2}) + \cos(\frac{\theta}{2}) \right) d\theta = 4\pi R \int^{\pi}_0 \left( \sin(\frac{\theta}{2}) + \cos(\frac{\theta}{2}) \right)d\theta

This is easily evaluated, yielding 4\pi R[-2\cos(\frac{\theta}{2})+2\sin(\frac{\theta}{2})]^{\pi}_0 = 16 \pi R. By our first formula, we obtain the average length
\frac{16 \pi R}{(2\pi)^2} = \frac{4R}{\pi} which indeed was your first answer.