- #1
SmartyPants
- 12
- 1
- TL;DR Summary
- I can derive the volume for a ring torus (a ring toroid of circular cross-section), but I'm struggling to do the same for [I]any[/I] elliptical toroid
Like the title and the summary suggest, I can derive the volume ##V=2\,\pi^{2}\,r^{2}\,R## for a ring torus - a doughnut-style toroid (one such that the major radius ##R## > the minor radius ##r##, and it therefore has a hole at the center) that is of circular cross-section. But I want to be able to prove the general case, that is, derive the volume of any elliptical ring toroid, including those of non-circular cross-section (those with an elliptical cross-section of non-zero eccentricity, and therefore have semi-major and semi-minor axes ##a\neq b##).
I run into a road block at a point in my integration where I have to make a trigonometric substitution. Specifically, I'm having trouble getting the upper bound of integration I want while making this change of variables from ##x## to ##\theta##. I had to do a trig substitution while deriving the volume of the ring torus (the one w/ circular cross-section) as well. ##\sin\theta## ended up being equal to 1, so ##\theta## (and therefore my upper bound) ended up being equal to ##\frac{\pi}{2}##, and everything worked out beautifully...
...not so with the one of elliptical cross-section. Unfortunately I don't really know how to show you where I'm hitting a roadblock without simply starting at the beginning. So I'll start by posting my successful derivation of the volume of the ring torus of circular cross-section first, and then post what I have so far for the derivation of the volume of a ring toroid of non-circular cross-section up to the point where I get stuck. I apologize in advance for the lengthiness of this post .
.
DERIVATION OF THE VOLUME OF AN ELLIPTICAL RING TORUS (A RING TOROID OF CIRCULAR CROSS-SECTION):
I started with a circle of radius ##r## in the ##xy##-plane whose center is at the point ##(0,R,0)##, where ##R>r## so that there is a hole at the center of the torus, doughnut-style:
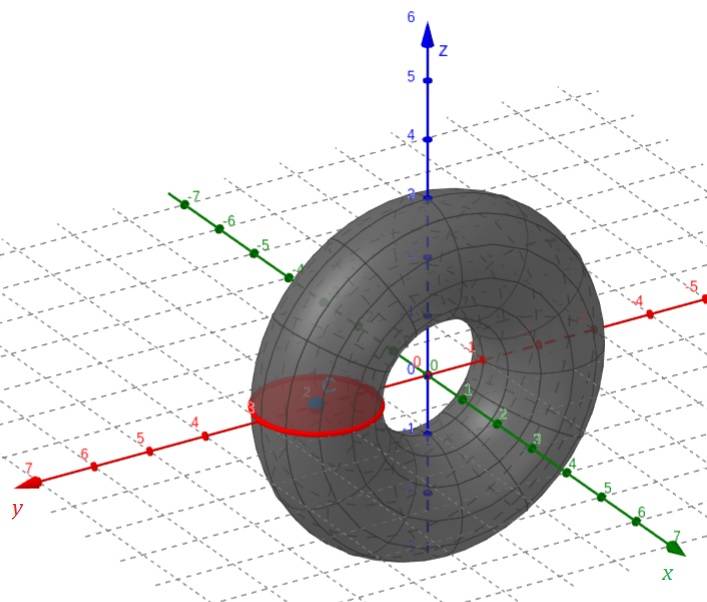
Since the implicit equation of a circle becomes two functions when y is solved for x explicitly (the upper and lower halves of the circle), what I did was revolve the upper half of the circle about the x-axis first, giving me the volume I labeled ##V_{1}##. I then did the same for the lower half, called it ##V_{2}##, and subtracted it from ##V_{1}## to get ##V_{torus}##. Starting with the equation of a circle and solving for ##y##, we have:
$$x^2+(y-R)^2=r^2\rightarrow (y-R)^2=r^2-x^2\rightarrow y-R=\pm\sqrt{r^2-x^2}\rightarrow y=+\sqrt{r^2-x^2}+R $$
Substituting in the function ##\sqrt{r^2-x^2}+R## for ##y## in the "solid of revolution" formula and evaluating, we have:
$$V_1=\int_{a}^{b}{\pi y^2\;dx}=\pi\int_{-r}^{r}{\left(\sqrt{r^2-x^2}+R\right)^2\;dx}$$ $$=2\pi\int_{0}^{r}{\left(\sqrt{r^2-x^2}+R\right)^2\;dx}=2\pi\int_{0}^{r}{\left(r^2-x^2+2R\sqrt{r^2-x^2}+R^2\right)\;dx}$$ $$=2\pi\int_{0}^{r}{r^2\mathrm{\ } dx}-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx+2\pi\int_{0}^{r}{2R\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\int_{0}^{r}{R^2\mathrm{\ } dx}$$ $$=2\pi\cdot r^2\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx+2\pi\cdot2R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\cdot R^2\int_{0}^{r}dx$$ $$=2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx+4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}$$
At this point I grouped the first two integrals together and evaluated third integral separately because it required a trigonometric substitution. I dealt with the first two integrals first:
$$2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx=2\pi\left(r^2+R^2\right)\left[x\right]{r\atop0}-2\pi\left[\frac{x^3}{3}\right]{r\atop0}}$$ $$=2\pi\left(r^2+R^2\right)\left(r-0\right)-2\pi\left(\frac{r^3}{3}-\frac{0^3}{3}\right)=2\pi r\left(r^2+R^2\right)-\frac{2\pi r^3}{3}$$ $$=2\pi r^3+2\pi rR^2-\frac{2\pi r^3}{3}=\mathbf{2}{\pi r}{R}^\mathbf{2}-\frac{\mathbf{4}{\pi}{r}^\mathbf{3}}{\mathbf{3}}$$
...and now for the integral that required a trig substitution:
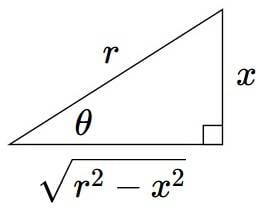
Here, I had to make another substitution: let ##u=2\theta\rightarrow du=2\ d\theta\rightarrow d\theta=\frac{1}{2}du##
$$\rightarrow4\pi r^2R\int_{0}^{\frac{\pi}{2}}{\frac{1}{2}\ d\theta}+4\pi r^2R\int_{0}^{\frac{\pi}{2}}{\frac{1}{2}cos\ 2\theta\ d\theta}=4\pi r^2R\cdot\frac{1}{2}\int_{0}^{\frac{\pi}{2}}d\theta+4\pi r^2R\cdot\frac{1}{2}\int_{0}^{\frac{\pi}{2}}{cos\ u\cdot\frac{1}{2}du}$$ $$=2\pi r^2R\int_{0}^{\frac{\pi}{2}}d\theta+4\pi r^2R\cdot\frac{1}{4}\int_{0}^{\frac{\pi}{2}}{cos\ u\ du}$$ $$=2\pi r^2R\left[\theta\right]{\frac{\pi}{2}\atop0}+\pi r^2R\left[sin\ u\right]{\frac{\pi}{2}\atop0}=2\pi r^2R\left[\theta\right]{\frac{\pi}{2}\atop0}+\pi r^2R\left[sin\ 2\theta\right]{\frac{\pi}{2}\atop0}$$ $$=2\pi r^2R\left(\frac{\pi}{2}-0\right)+\pi r^2R\left(sin\ \pi-sin\ 0\right)=2\pi r^2R\left(\frac{\pi}{2}\right)+\pi r^2R\left(0-0\right)=\pi^2r^2R+\pi r^2R\left(0\right)={\pi}^\mathbf{2}{r}^\mathbf{2}{R}$$
Putting things back together, we have:
$$\left(2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx}\right)+\left(4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}\right)$$ $$=2\pi{rR}^2-\frac{4\pi r^3}{3}+\pi^2r^2R$$ $$Thus, {V}_\mathbf{1}=\mathbf{2}{\pi}{{rR}}^\mathbf{2}-\frac{\mathbf{4}{\pi}{r}^\mathbf{3}}{\mathbf{3}}+{\pi}^\mathbf{2}{r}^\mathbf{2}{R}$$
Then I had to calculate the volume beneath the lower half of the circle ##y=-\sqrt{r^2-x^2}+R##:
$$V_2=\int_{a}^{b}{\pi y^2\;dx}=\pi\int_{-r}^{r}{\left(-\sqrt{r^2-x^2}+R\right)^2\;dx}=2\pi\int_{0}^{r}{\left(-\sqrt{r^2-x^2}+R\right)^2\;dx}$$ $$=2\pi\int_{0}^{r}{\left(r^2-x^2-2R\sqrt{r^2-x^2}+R^2\right)\;dx}$$ $$=2\pi\int_{0}^{r}{r^2\mathrm{\ } dx}-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx-2\pi\int_{0}^{r}{2R\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\int_{0}^{r}{R^2\mathrm{\ } dx}$$ $$=2\pi\cdot r^2\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx-2\pi\cdot2R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\cdot R^2\int_{0}^{r}dx$$ $$=2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx-4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}$$ ##\rightarrow## I already calculated these integrals in the previous step, so I already know that ##2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx}=2\pi rR^2-\frac{4\pi r^3}{3} ##, and I know that ##4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}=\pi^2r^2R##, but whereas I added these values together in the previous step, I have to subtract the latter from the former here:
$$\left(2\pi r R^2-\frac{4\pi r^3}{3}\right)-\left(\pi^2r^2R\right)$$
...and finally, I calculated ##V1-V2= Vtorus## and got:
$$2\pi{rR}^2-\frac{4\pi r^3}{3}+\pi^2r^2R-\left(2\pi r R^2-\frac{4\pi r^3}{3}-\pi^2r^2R\right)$$ $$=2\pi{rR}^2-\frac{4\pi r^3}{3}+\pi^2r^2R-2\pi{rR}^2+\frac{4\pi r^3}{3}+\pi^2r^2R=2\pi^2r^2R$$
OK...hopefully you're not so bored yet that that I've lost your attention . Now I'll post what I have so far for the derivation of the volume of a ring toroid of non-circular cross-section up to the point that I get stuck...
. Now I'll post what I have so far for the derivation of the volume of a ring toroid of non-circular cross-section up to the point that I get stuck...
DERIVATION OF THE VOLUME OF AN ELLIPTICAL PARABOLOID OF NON-CIRCULAR CROSS-SECTION:
I started with an ellipse of semi-major axis ##a## and semi-minor axis ##b## in the ##xy##-plane whose center is at the point ##(0,R,0)##, where ##R>a## (or ##b##, whichever semi-axis is parallel to the major axis) so that there is a hole at the center of the torus, doughnut-style. We have the same setup as before, the only difference being the shape of the toroid's cross-section:
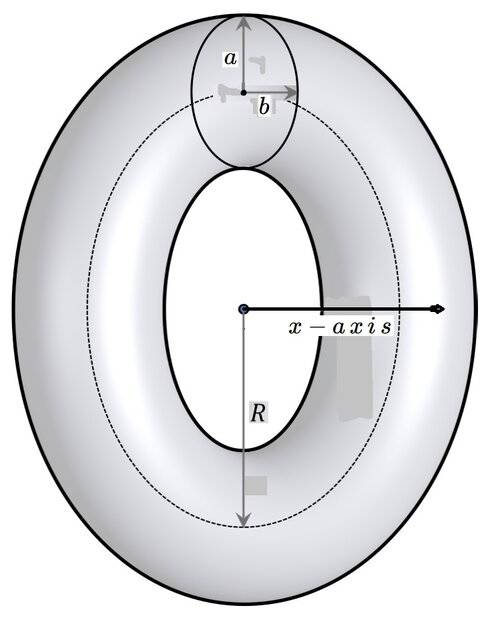
Since the implicit equation of an ellipse becomes two functions when y is solved for x explicitly (its upper and lower halves), what I did was revolve the upper half of the ellipse about the x-axis first, giving me the volume I labeled ##V_{1}##. I then did the same for the lower half, called it ##V_{2}##, and subtracted it from ##V_{1}## to get ##V_{toroid}##. Starting with the equation of an ellipse and solving for ##y##, we have:
$$\frac{x^2}{a^2}+\frac{\left(y-R\right)^2}{b^2}=1\rightarrow\frac{\left(y-R\right)^2}{b^2}=1-\frac{x^2}{a^2}\rightarrow\left(y-R\right)^2=b^2\left(1-\frac{x^2}{a^2}\right)$$ $$\rightarrow y-R=\pm\sqrt{b^2\left(1-\frac{x^2}{a^2}\right)}\rightarrow y=\pm b\sqrt{1-\frac{x^2}{a^2}}+R$$
Substituting in the function ##y=b\sqrt{1-\frac{x^2}{a^2}}+R## for ##y## in the "solid of revolution" formula and evaluating, we have:
$$V_1=\int_{a}^{b}{\pi y^2\;dx}=\pi\int_{-b}^{b}{\left(y=b\sqrt{1-\frac{x^2}{a^2}}+R\right)^2\;dx}=2\pi\int_{0}^{b}{\left(b\sqrt{1-\frac{x^2}{a^2}}+R\ \right)^2\;dx}$$ $$=2\pi\int_{0}^{b}{\left(b^2\left(1-\frac{x^2}{a^2}\right)+2b\sqrt{1-\frac{x^2}{a^2}}+R^2\right)\;dx}$$ $$=2\pi\int_{0}^{b}{b^2\left(1-\frac{x^2}{a^2}\right)dx}+2\pi\int_{0}^{b}{2b\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}+2\pi\int_{0}^{b}{R^2\mathrm{\ } dx}$$ $$=2\pi\cdot b^2\int_{0}^{b}{\left(1-\frac{x^2}{a^2}\right)dx+2\pi\cdot2b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}+2\pi\cdot R^2\int_{0}^{b}dx$$ $$=2\pi b^2\int_{0}^{b}{1\ dx-2\pi b^2\int_{0}^{b}\frac{x^2}{a^2}\ dx+4\pi b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}+2\pi R^2\int_{0}^{b}dx$$ $$=\left(2\pi b^2+2\pi R^2\right)\int_{0}^{b}{dx-2\pi b^2\cdot\frac{1}{a^2}\int_{0}^{b}x^2dx+4\pi b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}$$ $$=2\pi\left(b^2+R^2\right)\int_{0}^{b}{dx-\frac{2\pi b^2}{a^2}\int_{0}^{b}x^2dx+4\pi b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}$$
At this point I grouped the first two integrals together and evaluated third integral separately because it required a trigonometric substitution. I dealt with the first two integrals first:
$$2\pi\left(b^2+R^2\right)\int_{0}^{b}dx-\frac{2\pi b^2}{a^2}\int_{0}^{b}{x^2\mathrm{\ } dx=2\pi\left(b^2+R^2\right)\left[x\right]{b\atop0}-\frac{2\pi b^2}{a^2}\left[\frac{x^3}{3}\right]{b\atop0}}$$ $$=2\pi\left(b^2+R^2\right)\left(b-0\right)-\frac{2\pi b^2}{a^2}\left(\frac{b^3}{3}-\frac{0^3}{3}\right)=2\pi\left(b^2+R^2\right)\left(b\right)-\frac{2\pi b^2}{a^2}\left(\frac{b^3}{3}\right)$$ $$=2\pi b\left(b^2+R^2\right)-\frac{2\pi b^5}{{3a}^2}=2\pi b^3+2\pi bR^2-\frac{2\pi b^5}{{3a}^2}=\frac{6\pi{a^2b}^3}{{3a}^2}+2\pi bR^2-\frac{2\pi b^5}{{3a}^2}$$ $$=2\pi bR^2+\frac{6\pi{a^2b}^3-2\pi b^5}{{3a}^2}=\mathbf{2}{\pi b}{R}^\mathbf{2}+\mathbf{2}{\pi}{b}^\mathbf{3}\frac{\mathbf{3}{a}^\mathbf{2}-{b}^\mathbf{2}}{{\mathbf{3}{a}}^\mathbf{2}}$$
...and now for the integral that required a trig substitution:
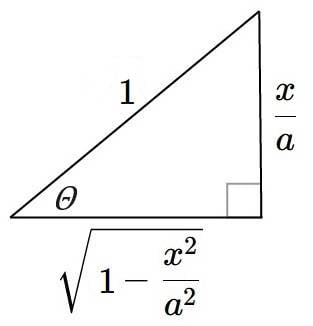
So that's it - I can't come up with a value that makes sense for the upper limit of my integral during a trig substitution and the associated change of variables from ##x## to ##\theta##. Any ideas on where to go from here? Apparently the volume of an elliptical ring toroid is ##{V}_{{toroid}}=2\pi^{2}abR## - almost the same as ##{V}_{{torus}}##, only ##r^2## gets replaced w/ ##ab##. I feel like I'm so close, yet so far...
Thanks in advance,
Eric
I run into a road block at a point in my integration where I have to make a trigonometric substitution. Specifically, I'm having trouble getting the upper bound of integration I want while making this change of variables from ##x## to ##\theta##. I had to do a trig substitution while deriving the volume of the ring torus (the one w/ circular cross-section) as well. ##\sin\theta## ended up being equal to 1, so ##\theta## (and therefore my upper bound) ended up being equal to ##\frac{\pi}{2}##, and everything worked out beautifully...
...not so with the one of elliptical cross-section. Unfortunately I don't really know how to show you where I'm hitting a roadblock without simply starting at the beginning. So I'll start by posting my successful derivation of the volume of the ring torus of circular cross-section first, and then post what I have so far for the derivation of the volume of a ring toroid of non-circular cross-section up to the point where I get stuck. I apologize in advance for the lengthiness of this post
DERIVATION OF THE VOLUME OF AN ELLIPTICAL RING TORUS (A RING TOROID OF CIRCULAR CROSS-SECTION):
I started with a circle of radius ##r## in the ##xy##-plane whose center is at the point ##(0,R,0)##, where ##R>r## so that there is a hole at the center of the torus, doughnut-style:
Since the implicit equation of a circle becomes two functions when y is solved for x explicitly (the upper and lower halves of the circle), what I did was revolve the upper half of the circle about the x-axis first, giving me the volume I labeled ##V_{1}##. I then did the same for the lower half, called it ##V_{2}##, and subtracted it from ##V_{1}## to get ##V_{torus}##. Starting with the equation of a circle and solving for ##y##, we have:
$$x^2+(y-R)^2=r^2\rightarrow (y-R)^2=r^2-x^2\rightarrow y-R=\pm\sqrt{r^2-x^2}\rightarrow y=+\sqrt{r^2-x^2}+R $$
Substituting in the function ##\sqrt{r^2-x^2}+R## for ##y## in the "solid of revolution" formula and evaluating, we have:
$$V_1=\int_{a}^{b}{\pi y^2\;dx}=\pi\int_{-r}^{r}{\left(\sqrt{r^2-x^2}+R\right)^2\;dx}$$ $$=2\pi\int_{0}^{r}{\left(\sqrt{r^2-x^2}+R\right)^2\;dx}=2\pi\int_{0}^{r}{\left(r^2-x^2+2R\sqrt{r^2-x^2}+R^2\right)\;dx}$$ $$=2\pi\int_{0}^{r}{r^2\mathrm{\ } dx}-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx+2\pi\int_{0}^{r}{2R\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\int_{0}^{r}{R^2\mathrm{\ } dx}$$ $$=2\pi\cdot r^2\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx+2\pi\cdot2R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\cdot R^2\int_{0}^{r}dx$$ $$=2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx+4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}$$
At this point I grouped the first two integrals together and evaluated third integral separately because it required a trigonometric substitution. I dealt with the first two integrals first:
$$2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx=2\pi\left(r^2+R^2\right)\left[x\right]{r\atop0}-2\pi\left[\frac{x^3}{3}\right]{r\atop0}}$$ $$=2\pi\left(r^2+R^2\right)\left(r-0\right)-2\pi\left(\frac{r^3}{3}-\frac{0^3}{3}\right)=2\pi r\left(r^2+R^2\right)-\frac{2\pi r^3}{3}$$ $$=2\pi r^3+2\pi rR^2-\frac{2\pi r^3}{3}=\mathbf{2}{\pi r}{R}^\mathbf{2}-\frac{\mathbf{4}{\pi}{r}^\mathbf{3}}{\mathbf{3}}$$
...and now for the integral that required a trig substitution:
- ##cos\ \theta=\frac{\sqrt{r^2-x^2}}{r}\rightarrow\sqrt{r^2-x^2}=r\ cos\ \theta##
- Also, ##sin\ \theta=\frac{x}{r}\rightarrow x=r\ sin\ \theta\rightarrow dx=r\ cos\ \theta\ d\theta##
- Also, when ##x=0##, ##sin\ \theta=\frac{0}{r}=0\rightarrow\theta=0## when ##sin\ \theta=0## (upper limit)
- Also, when ##x=r##, ##sin\ \theta=\frac{r}{r}=1\rightarrow\theta=\frac{\pi}{2}## when ##sin\ \theta=1## (lower limit)
$$4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}=4\pi R\int_{0}^{\frac{\pi}{2}}{r\ cos\ \theta\cdot r\ cos\ \theta\ d\theta}=4\pi R\int_{0}^{\frac{\pi}{2}}{{r^2cos}^2\ \theta\ d\theta}$$ ##=4\pi r^2R\int_{0}^{\frac{\pi}{2}}{{cos}^2\ \theta\ d\theta}=4\pi r^2R\int_{0}^{\frac{\pi}{2}}{\frac{1+cos\ 2\theta}{2}\ d\theta}## (via the half-angle formulas) $$=4\pi r^2R\int_{0}^{\frac{\pi}{2}}{\frac{1}{2}\ d\theta}+4\pi r^2R\int_{0}^{\frac{\pi}{2}}{\frac{1}{2}cos\ 2\theta\ d\theta}$$
Here, I had to make another substitution: let ##u=2\theta\rightarrow du=2\ d\theta\rightarrow d\theta=\frac{1}{2}du##
$$\rightarrow4\pi r^2R\int_{0}^{\frac{\pi}{2}}{\frac{1}{2}\ d\theta}+4\pi r^2R\int_{0}^{\frac{\pi}{2}}{\frac{1}{2}cos\ 2\theta\ d\theta}=4\pi r^2R\cdot\frac{1}{2}\int_{0}^{\frac{\pi}{2}}d\theta+4\pi r^2R\cdot\frac{1}{2}\int_{0}^{\frac{\pi}{2}}{cos\ u\cdot\frac{1}{2}du}$$ $$=2\pi r^2R\int_{0}^{\frac{\pi}{2}}d\theta+4\pi r^2R\cdot\frac{1}{4}\int_{0}^{\frac{\pi}{2}}{cos\ u\ du}$$ $$=2\pi r^2R\left[\theta\right]{\frac{\pi}{2}\atop0}+\pi r^2R\left[sin\ u\right]{\frac{\pi}{2}\atop0}=2\pi r^2R\left[\theta\right]{\frac{\pi}{2}\atop0}+\pi r^2R\left[sin\ 2\theta\right]{\frac{\pi}{2}\atop0}$$ $$=2\pi r^2R\left(\frac{\pi}{2}-0\right)+\pi r^2R\left(sin\ \pi-sin\ 0\right)=2\pi r^2R\left(\frac{\pi}{2}\right)+\pi r^2R\left(0-0\right)=\pi^2r^2R+\pi r^2R\left(0\right)={\pi}^\mathbf{2}{r}^\mathbf{2}{R}$$
Putting things back together, we have:
$$\left(2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx}\right)+\left(4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}\right)$$ $$=2\pi{rR}^2-\frac{4\pi r^3}{3}+\pi^2r^2R$$ $$Thus, {V}_\mathbf{1}=\mathbf{2}{\pi}{{rR}}^\mathbf{2}-\frac{\mathbf{4}{\pi}{r}^\mathbf{3}}{\mathbf{3}}+{\pi}^\mathbf{2}{r}^\mathbf{2}{R}$$
Then I had to calculate the volume beneath the lower half of the circle ##y=-\sqrt{r^2-x^2}+R##:
$$V_2=\int_{a}^{b}{\pi y^2\;dx}=\pi\int_{-r}^{r}{\left(-\sqrt{r^2-x^2}+R\right)^2\;dx}=2\pi\int_{0}^{r}{\left(-\sqrt{r^2-x^2}+R\right)^2\;dx}$$ $$=2\pi\int_{0}^{r}{\left(r^2-x^2-2R\sqrt{r^2-x^2}+R^2\right)\;dx}$$ $$=2\pi\int_{0}^{r}{r^2\mathrm{\ } dx}-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx-2\pi\int_{0}^{r}{2R\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\int_{0}^{r}{R^2\mathrm{\ } dx}$$ $$=2\pi\cdot r^2\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx-2\pi\cdot2R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}+2\pi\cdot R^2\int_{0}^{r}dx$$ $$=2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx-4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}}$$ ##\rightarrow## I already calculated these integrals in the previous step, so I already know that ##2\pi\left(r^2+R^2\right)\int_{0}^{r}dx-2\pi\int_{0}^{r}{x^2\mathrm{\ } dx}=2\pi rR^2-\frac{4\pi r^3}{3} ##, and I know that ##4\pi R\int_{0}^{r}{\sqrt{r^2-x^2}\mathrm{\ } dx}=\pi^2r^2R##, but whereas I added these values together in the previous step, I have to subtract the latter from the former here:
$$\left(2\pi r R^2-\frac{4\pi r^3}{3}\right)-\left(\pi^2r^2R\right)$$
...and thus, ##{V}_\mathbf{2}=\mathbf{2}{\pi}{{rR}}^\mathbf{2}-\frac{\mathbf{4}{\pi}{r}^\mathbf{3}}{\mathbf{3}}-{\pi}^\mathbf{2}{r}^\mathbf{2}{R}##.
...and finally, I calculated ##V1-V2= Vtorus## and got:
$$2\pi{rR}^2-\frac{4\pi r^3}{3}+\pi^2r^2R-\left(2\pi r R^2-\frac{4\pi r^3}{3}-\pi^2r^2R\right)$$ $$=2\pi{rR}^2-\frac{4\pi r^3}{3}+\pi^2r^2R-2\pi{rR}^2+\frac{4\pi r^3}{3}+\pi^2r^2R=2\pi^2r^2R$$
...and thus, ##{V}_{{torus}}=\mathbf{2}{\pi}^\mathbf{2}{r}^\mathbf{2}{R}##
OK...hopefully you're not so bored yet that that I've lost your attention
DERIVATION OF THE VOLUME OF AN ELLIPTICAL PARABOLOID OF NON-CIRCULAR CROSS-SECTION:
I started with an ellipse of semi-major axis ##a## and semi-minor axis ##b## in the ##xy##-plane whose center is at the point ##(0,R,0)##, where ##R>a## (or ##b##, whichever semi-axis is parallel to the major axis) so that there is a hole at the center of the torus, doughnut-style. We have the same setup as before, the only difference being the shape of the toroid's cross-section:
Since the implicit equation of an ellipse becomes two functions when y is solved for x explicitly (its upper and lower halves), what I did was revolve the upper half of the ellipse about the x-axis first, giving me the volume I labeled ##V_{1}##. I then did the same for the lower half, called it ##V_{2}##, and subtracted it from ##V_{1}## to get ##V_{toroid}##. Starting with the equation of an ellipse and solving for ##y##, we have:
$$\frac{x^2}{a^2}+\frac{\left(y-R\right)^2}{b^2}=1\rightarrow\frac{\left(y-R\right)^2}{b^2}=1-\frac{x^2}{a^2}\rightarrow\left(y-R\right)^2=b^2\left(1-\frac{x^2}{a^2}\right)$$ $$\rightarrow y-R=\pm\sqrt{b^2\left(1-\frac{x^2}{a^2}\right)}\rightarrow y=\pm b\sqrt{1-\frac{x^2}{a^2}}+R$$
Substituting in the function ##y=b\sqrt{1-\frac{x^2}{a^2}}+R## for ##y## in the "solid of revolution" formula and evaluating, we have:
$$V_1=\int_{a}^{b}{\pi y^2\;dx}=\pi\int_{-b}^{b}{\left(y=b\sqrt{1-\frac{x^2}{a^2}}+R\right)^2\;dx}=2\pi\int_{0}^{b}{\left(b\sqrt{1-\frac{x^2}{a^2}}+R\ \right)^2\;dx}$$ $$=2\pi\int_{0}^{b}{\left(b^2\left(1-\frac{x^2}{a^2}\right)+2b\sqrt{1-\frac{x^2}{a^2}}+R^2\right)\;dx}$$ $$=2\pi\int_{0}^{b}{b^2\left(1-\frac{x^2}{a^2}\right)dx}+2\pi\int_{0}^{b}{2b\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}+2\pi\int_{0}^{b}{R^2\mathrm{\ } dx}$$ $$=2\pi\cdot b^2\int_{0}^{b}{\left(1-\frac{x^2}{a^2}\right)dx+2\pi\cdot2b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}+2\pi\cdot R^2\int_{0}^{b}dx$$ $$=2\pi b^2\int_{0}^{b}{1\ dx-2\pi b^2\int_{0}^{b}\frac{x^2}{a^2}\ dx+4\pi b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}+2\pi R^2\int_{0}^{b}dx$$ $$=\left(2\pi b^2+2\pi R^2\right)\int_{0}^{b}{dx-2\pi b^2\cdot\frac{1}{a^2}\int_{0}^{b}x^2dx+4\pi b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}$$ $$=2\pi\left(b^2+R^2\right)\int_{0}^{b}{dx-\frac{2\pi b^2}{a^2}\int_{0}^{b}x^2dx+4\pi b\int_{0}^{b}{\sqrt{1-\frac{x^2}{a^2}}\mathrm{\ } dx}}$$
At this point I grouped the first two integrals together and evaluated third integral separately because it required a trigonometric substitution. I dealt with the first two integrals first:
$$2\pi\left(b^2+R^2\right)\int_{0}^{b}dx-\frac{2\pi b^2}{a^2}\int_{0}^{b}{x^2\mathrm{\ } dx=2\pi\left(b^2+R^2\right)\left[x\right]{b\atop0}-\frac{2\pi b^2}{a^2}\left[\frac{x^3}{3}\right]{b\atop0}}$$ $$=2\pi\left(b^2+R^2\right)\left(b-0\right)-\frac{2\pi b^2}{a^2}\left(\frac{b^3}{3}-\frac{0^3}{3}\right)=2\pi\left(b^2+R^2\right)\left(b\right)-\frac{2\pi b^2}{a^2}\left(\frac{b^3}{3}\right)$$ $$=2\pi b\left(b^2+R^2\right)-\frac{2\pi b^5}{{3a}^2}=2\pi b^3+2\pi bR^2-\frac{2\pi b^5}{{3a}^2}=\frac{6\pi{a^2b}^3}{{3a}^2}+2\pi bR^2-\frac{2\pi b^5}{{3a}^2}$$ $$=2\pi bR^2+\frac{6\pi{a^2b}^3-2\pi b^5}{{3a}^2}=\mathbf{2}{\pi b}{R}^\mathbf{2}+\mathbf{2}{\pi}{b}^\mathbf{3}\frac{\mathbf{3}{a}^\mathbf{2}-{b}^\mathbf{2}}{{\mathbf{3}{a}}^\mathbf{2}}$$
...and now for the integral that required a trig substitution:
- ##cos\ \theta=\frac{\sqrt{1-\frac{x^2}{a^2}}}{1}\rightarrow\sqrt{1-\frac{x^2}{a^2}}=cos\ \theta##
- Also, ##sin\ \theta=\frac{\frac{x}{a}}{1}=\frac{x}{a}\rightarrow x=a\ sin\ \theta\rightarrow dx=a\ cos\ \theta\ d\theta##
- Also, when ##x=0, sin\ \theta=\frac{0}{a}=0\rightarrow\theta=0## when ##sin\ \theta=0## (upper limit)
- Also, when ##x=b, sin\ \theta=\frac{b}{a}=?\rightarrow\theta=?## when ##sin\ \theta=\frac{b}{a}## (lower limit)
So that's it - I can't come up with a value that makes sense for the upper limit of my integral during a trig substitution and the associated change of variables from ##x## to ##\theta##. Any ideas on where to go from here? Apparently the volume of an elliptical ring toroid is ##{V}_{{toroid}}=2\pi^{2}abR## - almost the same as ##{V}_{{torus}}##, only ##r^2## gets replaced w/ ##ab##. I feel like I'm so close, yet so far...
Thanks in advance,
Eric