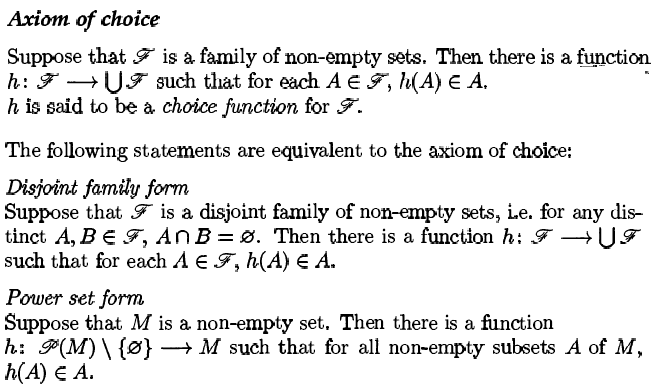SUMMARY
The discussion centers on the proof of the Axiom of Choice, specifically the transition from a general power set ##\mathscr{P}(M)## to a disjoint family ##\mathscr{F}##. Participants debate the validity of a "trick" used to apply the disjoint family form to derive the power set form. The consensus is that defining ##\mathscr{F}## allows for the application of the disjoint family theorem, thereby enabling the deduction of the power set form. The conversation highlights the necessity of precise definitions in understanding the proof's structure.
PREREQUISITES
- Understanding of set theory concepts, including power sets and disjoint families.
- Familiarity with the Axiom of Choice and its implications in mathematical proofs.
- Knowledge of formal logic and proof techniques in mathematics.
- Ability to interpret mathematical notation, particularly set notation like ##\mathscr{P}(M)## and ##\mathscr{F}##.
NEXT STEPS
- Study the formal definitions of power sets and disjoint families in set theory.
- Examine the Axiom of Choice and its various formulations and implications.
- Learn about proof techniques in set theory, focusing on how to transition between different forms of mathematical statements.
- Explore examples of applying the disjoint family theorem in mathematical proofs.
USEFUL FOR
Mathematicians, students of set theory, and anyone interested in the foundational aspects of mathematical logic and proofs related to the Axiom of Choice.