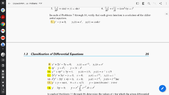
MHB -b.1.3.12 .... is a solution of the DE

  • Thread starter Thread starter karush
  • Start date Start date
Click For Summary
The discussion focuses on verifying that the functions y_2(t) = t^{-2}ln(t) and y_1(t) = t^{-2} are solutions to the differential equation t^2y'' + 5ty' + 4y = 0. The verification process involves calculating the derivatives of y_1(t) and substituting them into the equation, which simplifies to zero, confirming that y_1(t) is indeed a solution. Participants express that while the verification is straightforward, solving the equation can be tedious. There is a suggestion that the forum, MHB, should consider writing textbooks due to the complexity of the examples discussed. Overall, the emphasis is on the verification process rather than solving the differential equation itself.
karush
Gold Member
MHB
Messages
3,240
Reaction score
5
1632528196874.png
####
#12 hope I rewrote the problem ok

Verify that $y_2(t)=t^{-2}\ln t\quad y_1(t)=t^{-2}$ is a solution of $t^2y''+5ty'+4y=0$
think the first steop is to compose a charactistic equation using r
 

Attachments

  • 1632528147724.png
    1632528147724.png
    34.9 KB · Views: 154
Physics news on Phys.org
$y_1(t) = t^{-2} \implies y'_1(t) = -2t^{-3} \implies y''_1(t) = 6t^{-4}$

$t^2 \cdot 6t^{-4} + 5t \cdot(-2t^{-3}) + 4 \cdot t^{-2} = 6t^{-2} - 10t^{-2} + 4t^{-2} = 0$

verified
 
so that is how it is done...
the examples were pretty mind numbing compared

I really think MHB should write textbooks...
 
karush said:
so that is how it is done...
the examples were pretty mind numbing compared

I really think MHB should write textbooks...
You are merely supposed to verify the solutions. So just plug them in. Solving the equation, on the other hand, can be a bit mind numbing until you get used to it.

-Dan
 

Similar threads

MHB Solving IVP $y''-y=0$ with $y_1,y_2$
  • · Replies 5 ·
Replies
5
Views
2K
MHB -16.1 Find the general solution to the system of DE
  • · Replies 2 ·
Replies
2
Views
2K
MHB -1.8.17 initial value then find C
  • · Replies 11 ·
Replies
11
Views
2K
MHB Is the given function a solution of the differential equation?
  • · Replies 3 ·
Replies
3
Views
2K
MHB Differential Equations - Bernoulli equation
  • · Replies 3 ·
Replies
3
Views
4K
Undergrad Solving Differential Equation Using Reduction of Order
  • · Replies 2 ·
Replies
2
Views
4K
Undergrad Solution of delayed forcing function
  • · Replies 5 ·
Replies
5
Views
4K
Undergrad On error estimates of approximate solutions
  • · Replies 1 ·
Replies
1
Views
3K
Undergrad Verifying properties of Green's function
  • · Replies 1 ·
Replies
1
Views
3K
MHB Verify Solutions of Differential Equation y''-y=0
  • · Replies 12 ·
Replies
12
Views
3K