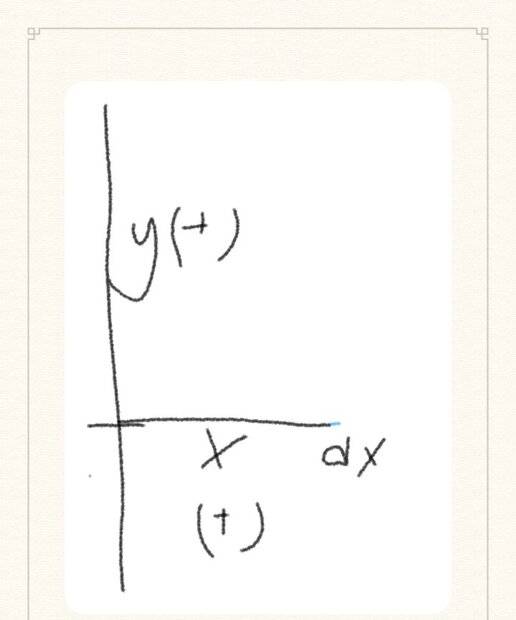SUMMARY
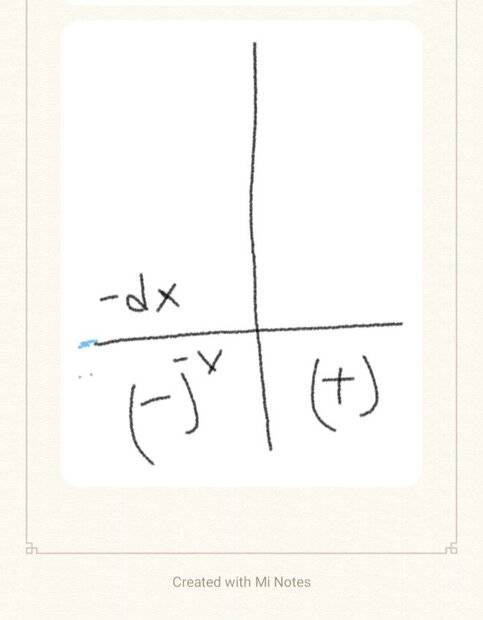
The discussion centers on the concept of negative infinitesimals in calculus, specifically in relation to the coordinate plane and mechanics. Participants confirm that negative infinitesimals, denoted as ##-\varepsilon##, exist and can be used in mathematical expressions. The conversation highlights that while infinitesimals are commonly represented as positive values, they can also take on negative values, particularly in the context of equilibrium conditions in mechanics. The Hyperreals are mentioned as a field where every element, including infinitesimals, has an additive inverse.
PREREQUISITES
- Understanding of calculus concepts, particularly derivatives and infinitesimals.
- Familiarity with the coordinate plane and basic mechanics principles.
- Knowledge of the Hyperreal number system and its properties.
- Basic algebraic manipulation involving positive and negative quantities.
NEXT STEPS
- Research the properties and applications of Hyperreal numbers in calculus.
- Study the role of infinitesimals in differential equations and their implications in mechanics.
- Explore the concept of limits and how they relate to infinitesimals in mathematical analysis.
- Learn about the formal definitions and uses of positive and negative infinitesimals in non-standard analysis.
USEFUL FOR
Mathematicians, physics students, and anyone interested in advanced calculus concepts, particularly those exploring the foundations of infinitesimals and their applications in mechanics.