theBEAST
- 361
- 0
Conservation of momentum does not hold true?
Here is the problem. State 2 is shown in the picture, it is right before impact. State 3 is after impact.
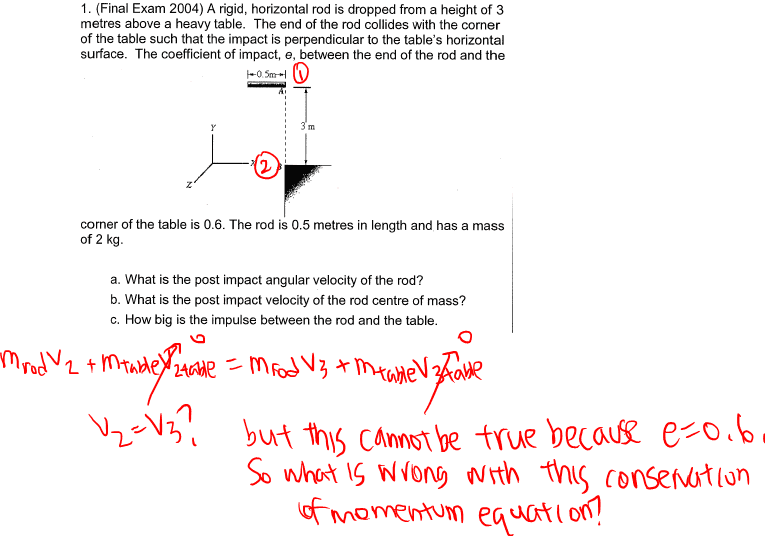
I used conservation of momentum of the entire system (rod and table. However as you can see it shows us that the rod has the same momentum before and after the impact. This is impossible because e=0.6. Why is it that my conservation equation does not hold?
Homework Statement
Here is the problem. State 2 is shown in the picture, it is right before impact. State 3 is after impact.
I used conservation of momentum of the entire system (rod and table. However as you can see it shows us that the rod has the same momentum before and after the impact. This is impossible because e=0.6. Why is it that my conservation equation does not hold?
Last edited: