Undergrad How does the residue factorization form arise in BCFW recursion in QFT?

Click For Summary
The discussion centers on the residue factorization form in BCFW recursion within quantum field theory (QFT). Participants reference various sources, including Britto's work and texts by Zee, Schwarz, and Huang, to explore how the residue at a pole manifests in this specific factorization. Two primary methods to demonstrate the factorization of amplitudes at simple poles are highlighted: an ancient proof based on S-matrix properties and a more recent local field theoretic proof found in Weinberg's text. The conversation emphasizes the importance of understanding these proofs to grasp the underlying principles of QFT. Overall, the factorization form is crucial for analyzing scattering amplitudes in quantum field theory.
Lapidus
Messages
344
Reaction score
12
Below is a snipet from http://file:///C:/Users/Christian.Hollersen/Downloads/Britto_2011_2%20(1).pdf of Britto. Similar explanation can be found in the QFT books of Zee, Schwarz or the Scattering Amplitude text of Huang. Or any other text that covers BCFW recursion. My dumb question: how and why does the residue at this pole take this funny factorization form? (For clarifcation: residue is the just the word QFT people use for the numerator of a rational function with a simple pole, right?)

bcwf.PNG


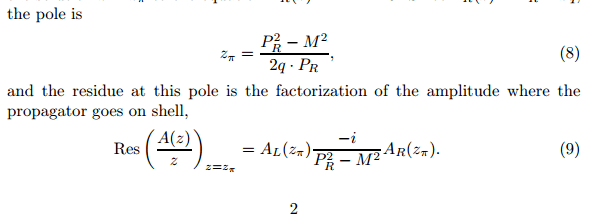
Thank you!
 
Last edited by a moderator:
Physics news on Phys.org
There are at least two ways to show the factorization of amplitudes on simple poles. An ancient proof using only properties of the S-matirx (analyticity, unitarity and cluster decomposition) can be found in Eden et al. "The Analytic S-matrix" sec. 4.5. For a more recent discussion see the nice review by Conde

http://pos.sissa.it/archive/conferences/201/005/Modave 2013_005.pdf

Alternatively there is a more local field theoretic proof given in Weinberg "The Quantum Theory of Fields Vol 1." sec. 10.2.
 

Thread 'Questioning the timescape model'

"Supernovae evidence for foundational change to cosmological models" https://arxiv.org/pdf/2412.15143 The paper claims: We compare the standard homogeneous cosmological model, i.e., spatially flat ΛCDM, and the timescape cosmology which invokes backreaction of inhomogeneities. Timescape, while statistically homogeneous and isotropic, departs from average Friedmann-Lemaître-Robertson-Walker evolution, and replaces dark energy by kinetic gravitational energy and its gradients, in explaining...
View full post »