AspiringPhysicist12
- 16
- 6
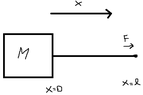
- Homework Statement
- A uniform rope of mass m and length l is attached to a block of
mass M. The rope is pulled with force F. Find the tension at distance
x from the end of the rope. Neglect gravity.
- Relevant Equations
- T(0) = T(L) = Ma
We have the string's mass constraint m(x) = m(x/L). The block is accelerated right by force T(x=0) = Ma, where a = F / m + M.
But at the point where the force is applied (i.e. x = L), I believe we have m(L/L)a = ma = F - T(L). But this would imply T(L) = F - ma = F - m(F / m + M) = F(M / m + M) = Ma. I know it doesn't make sense to have T(0) = T(L) since the rope has mass, but what am I doing wrong here?
But at the point where the force is applied (i.e. x = L), I believe we have m(L/L)a = ma = F - T(L). But this would imply T(L) = F - ma = F - m(F / m + M) = F(M / m + M) = Ma. I know it doesn't make sense to have T(0) = T(L) since the rope has mass, but what am I doing wrong here?