A Blue-Eye Paradox: Solution Not Unique

[D H]

So all islanders know that {all the islanders know that [someone has blue eyes]}.

This is mutual knowledge, but it is not common knowledge.

So if there are at least 3 islanders with blue eyes, then all islanders know that {all the islanders know that [someone has blue eyes]} - no need for a prophetic announcement.

Yes, there is. This announcement is the common knowledge that starts the countdown. There is a big difference between mutual knowledge and common knowledge.

I haven't seen the post that explains the version of this problem that is being discussed, and there are so many variations of this problem. A partial list:

• Terence Tao's version, posted here, here, and here. This version involves an island populated with tribespeople with various eye colors. It is forbidden to discuss eye color because someone who does discover the color of their eyes must commit suicide at noon for all to see. But then some blue-eyed foreigner visits to the island and tells the entire tribe “how unusual it is to see another blue-eyed person like myself in this region of the world.”
• https://www.physics.harvard.edu/uploads/files/undergrad/probweek/prob2.pdf. Then you visit the island and on your departure you tell the dragons that at least one has beautiful green eyes.
• A mathematics department populated with arrogant mathematicians, each of whom think they are infallible but must resign if they find they have published a paper containing an error. One day, a visiting mathematician announces “Someone here has made a mistake.”
• A group of people eat barbecued spare ribs, some of whom have barbecue sauce on their faces. The cook says “At least one of you has barbecue sauce on her face. I will ring the dinner bell over and over, until anyone who is messy has wiped her face. Then I will serve dessert.”

In all of these examples, there is a trigger that creates common knowledge that starts a countdown. The final link is part of a very nice article on common knowledge at the Stanford Encyclopedia of Philosophy. This article clearly distinguishes between mutual knowledge and common knowledge.

 

[lukesfn]

Although, I am not sure everybody quite understood the point I was bringing up, I'm pretty comfortable with my understanding of the puzzle and the paradox now. If applying the same inductive logic, the monks may all decide to leave, but if applying detective logic, they may all decide to stay. I don't see how inductive logic can be seen as perfect logic, therefore, with the set of assumptions I would choose, all monks would stay. I think this puzzle is an example of the flaws of inductive logic and the paradoxes it can create.

 

[.Scott]

Although, I am not sure everybody quite understood the point I was bringing up, I'm pretty comfortable with my understanding of the puzzle and the paradox now. If applying the same inductive logic, the monks may all decide to leave, but if applying detective logic, they may all decide to stay. I don't see how inductive logic can be seen as perfect logic, therefore, with the set of assumptions I would choose, all monks would stay. I think this puzzle is an example of the flaws of inductive logic and the paradoxes it can create.

The logic they use is entirely deductive.
If there was only one blue-eyed monk and the (truthful) guru declares that there is a blue-eyed monk, that one blue-eyed monk would deduce it was himself by eliminating all other possibilities. I'm sure you can work out the problem with two blue-eye monks as well - using exclusively deductive reasoning.

 

[Heinera]

Many of the recursion statements in this thread about monks knowing about other monks are either wrong or irrelevant - and are effectively straw horses in the discussion.

I don't entirely agree that recursive statements are irrelevant in this problem. For instance, the guru could make the suicide moment happen one step earlier by saying "there is at least one monk with blue eyes, and everybody knew that", etc.

 

[lukesfn]

If there was only one blue-eyed monk and the (truthful) guru declares that there is a blue-eyed monk, that one blue-eyed monk would deduce it was himself by eliminating all other possibilities. I'm sure you can work out the problem with two blue-eye monks as well - using exclusively deductive reasoning.

What if there was only one blue-eyed monk and the guru didn't speak?

Anyway, I think we are going around in circles and I am not sure how to explain my self better then I already have.

 

[Andreas C]

What if there was only one blue-eyed monk and the guru didn't speak?

Anyway, I think we are going around in circles and I am not sure how to explain my self better then I already have.

Nothing would happen then. If the guru didn't speak, nothing would happen. But since he does speak, he triggers the events.

The problem is not a paradox. It's a simple application of deductive logic for 3 persons, I agree, it seemingly gets more complicated and counter intuitive with more, but that doesn't mean anything. Of course, it's not stated very well, because the monks/islanders may or may not choose the same strategy, if we are to accept this solution we have to determine if there are no other solutions.

 

[forcefield]

But if the priest makes a declaration, then he knows that on the second opportunity the "2" theory will be tested.

That's a bit vague. I agree that recursion like "everyone knows that everyone knows that everyone knows" is not needed but it is a simple way to express that "A knows that B knows that C knows" and it's permutations.

 

[stevendaryl]

This is obviously a mathematical problem (at least once you've clarified the assumptions and the reasoning), but from my messing around, it seems notoriously difficult to formulate mathematically. One way is to use modal propositional logic.

Let B_1, B_2, ... be propositional variables with the interpretation that B_n means "islander number n has blue eyes". Let K_1, K_2, ... be modal operators with the interpretation that K_n P means "islander number n believes P".

Then we would need to axiomatize how these modal operators work. Something along the lines of:

For i \neq j,
B_i \leftrightarrow K_j B_i (Everybody knows whether or not everybody else has blue eyes)

And then there would be rules of inference of the form:

(K_n A) \wedge (K_n (A \rightarrow B)) \rightarrow K_n B

This seems enormously complicated. An alternative approach is to use graphs to represent possible worlds and their connections. Let a closed circle represent a possible world. Inside the circle, we list all the ID numbers of islanders with blue eyes. For each j, we draw an arrow from world W_1 to world W_2 if islander number j in world W_1 believes that he might be in world W_2.

For a simple example, imagine a world with two islanders. Here are shown 4 possible worlds: (W1) No blue-eyed people, (W2) Islander #1 has blue eyes, (W3) Islander #2 has blue eyes, and (W4) Both have blue eyes. In world W1, islander #2 believes that he might be in worlds W1 or W3, and islander #1 believes he might be in worlds W1 or W2.

Now, to simplify things, I'm going assume that:

• All blue-eyed islanders are indistinguishable. They believe the same things (or analogous things).
• All non-blue-eyed islanders are indistinguishable.
• The beliefs are completely determined by the objective facts (how many people with what colored eyes there are). So there can't be two worlds with the same number of blue-eyed and non-blue-eyed people, but differ in what people believe is possible.
• There are the same number of islanders in every possible world.

In light of these assumptions, we can characterize a world by the number of blue-eyed individuals in it. For definiteness, let's assume there are 3 islanders. Then we can characterize the situation by a sequence of graphs, one graph per day. On day -1, nobody knows anything except what they can see (and what they can deduce about what other people can see). On day 0, all the people in all possible worlds are told that there is at least one blue-eyed person. In any possible world, if a blue-eyed person can deduce that he is blue-eyed, then he kills himself. On day 1, in every possible world, if someone sees that a blue-eyed person is still alive, he deduces that that person did not deduce that he had blue eyes. Etc.

To say that someone deduces some fact means that that fact is true in every world that he considers possible.

Since all blue-eyed people believe the same thing, we will just use blue arrows to represent what blue-eyed people believe, and brown arrows to represent what non-blue-eyed people believe. So here is the sequence of situations (where a situation is an entire connected set of possible worlds corresponding to a day)

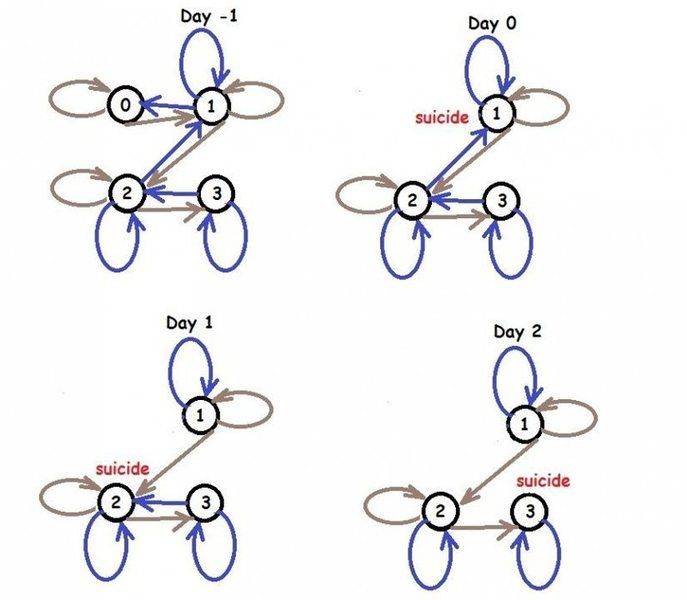
• On Day -1, blue-eyed people in any possible world believe that they are either in their actual world, or one with one fewer blue-eyed person (because they consider it possible that their own eyes are not blue). Non-blue-eyed people believe that they are either in their actual world, or one with one more blue-eyed person.
• On Day 0, it is announced (in every possible world) that there is at least one blue-eyed person. This eliminates the possible world with 0 blue-eyed people. So the graph of possible worlds is changed so that there is no blue arrow out of the world with 1 blue-eyed person. So the blue-eyed person in that world knows what world they are in, and so know that they have blue eyes, and so they commit suicide.
  
• On Day 1, in the possible world in which there are 2 blue-eyed people, they can see that nobody committed suicide. So that means that they do not live in the world with 1 blue-eyed person. So that arrow is eliminated, and they know exactly what world they are in--the one with 2 blue-eyed people. So they commit suicide.
• On Day 2, in the possible world in which there are 3 blue-eyed people, they can see that nobody committed suicide, so that means there are 3 blue-eyed people. So they commit suicide.

 

[.Scott]

it seems notoriously difficult to formulate mathematically

I agree. Or as I said before, to try to make a step-by-step statement about what every monk knows about every other monk ...
But what's wrong with the logic in post #100?

Now, to simplify things, I'm going assume that:

• All blue-eyed islanders are indistinguishable. They believe the same things (or analogous things).
• All non-blue-eyed islanders are indistinguishable.

You can treat the blue-eyed islanders as equivalent, but they are absolutely not "indistinguishable". It is critical to the logic that they be absolutely distinguishable so that each blue-eyed can determine that he is dealing with the same group of individuals at every event.

The non-blue-eyed islanders are irrelevant. You can have as many as you wish without effecting the logic. As I said before, they are only "furnishings".

 

[.Scott]

I don't entirely agree that recursive statements are irrelevant in this problem. For instance, the guru could make the suicide moment happen one step earlier by saying "there is at least one monk with blue eyes, and everybody knew that", etc.

No. But he could make it happen one step earlier by saying that he sees at least 2 blue-eyed monks. The statement "there is at least one blue-eyed monk" is a very specific trigger to a very specific sequence.

 

[.Scott]

That's a bit vague. I agree that recursion like "everyone knows that everyone knows that everyone knows" is not needed but it is a simple way to express that "A knows that B knows that C knows" and it's permutations.

OK, how's this:
Let $T_n$ represent the theory that there are $n$ blue-eyed monks on the island.
Let "day" represent the passing of an opportunity to commit suicide (or leave the island, depending on the story).
Whenever there is the credible statement: $~T_0$, then on the next day, either there will either be a suicide ($T_1$) or not. If there is not, it will prove $~T_1$. This is because if $T_1$, then that only blue-eyed monk knows $T_0 or T_1$, so with $~T_0$ he can deduce $T_1$ and that he is that 1. If no one commits suicide after day 1, that proves $~T_1$.

This logic holds even if other information already demonstrates $~T_0$ because this new declaration allows all the blue-eyed monks to know that $~T_0$ was given to all monks on the same day in a way that makes $~T_1$ deductible on the next day.

 

[.Scott]

What if there was only one blue-eyed monk and the guru didn't speak?

Anyway, I think we are going around in circles and I am not sure how to explain my self better then I already have.

Using the notation in my previous post, that monk knows $T_0 or T_1$, all other monks know $T_1 or T_2$. Without new information, such as the statement $~T_0$, nothing happens.

 

[stevendaryl]

You can treat the blue-eyed islanders as equivalent, but they are absolutely not "indistinguishable". It is critical to the logic that they be absolutely distinguishable so that each blue-eyed can determine that he is dealing with the same group of individuals at every event.

Okay, well I'm assuming that the population is fixed (other than deaths by suicide).

The non-blue-eyed islanders are irrelevant.

Not quite. For the puzzle to work, a blue-eyed islander has to consider it possible that his eyes are non-blue. So in my possible-worlds semantics of the puzzle, every world has the same total number of islanders, but differ in how many are blue-eyed.

 

[256bits]

but differ in how many are blue-eyed.

The number of non-blue-eyed islanders should be irrelevant. In the puzzle given, the non blues could be 1, 10, 1000,...
( Oh that was already stated )
What one has to consider is YOU as an islander, who does not know his eye color, and the deductive process to go through while perceiving only the blue-eyed and determining if your color is blue or non-blue. All the other blue-eyed will go through the same process. If you are blue-eyed then you are included in the blue eyed deductive process. If you are non-blue then you become irrelevant to the blues. As a brown, You can keep on doing Case A but it does not get you off the island.

Case A You are brown, but you don't know it but are hoping for the chance to leave which never comes.
EX1 1 blue eyed Jane - Jane sees no other blue so she is it. You see her leave on Day 1 so you are non-blue
Ex 2 2 eyed blue - Jane sees 1 blue and Sally sees 1 blue. You see 2 blue. Jane, Sally leave on Day 2. You are non-blue.
etc

Case B You are Blue, but don't know it and are hoping. eventually your chance to leave will come.
Ex 1 Jane, You blue. You both see one blue. She doesn'y leave on Day 1, so you and her deduce you are both blue, and you both leave on Day 2
Ex 2 Jane, Sally, You blue. All see 2 blue. Nobody leaves on Day 1, or Day 2, so all deduce they are blue and leave on Day 3.
etc.

 

[lukesfn]

I realized I keep confusing my self. I've been suffering a cold, and my ability to think clearly keeps abandoning me, and I have difficult even explaining what I am trying to understand.

 

[stevendaryl]

The number of non-blue-eyed islanders should be irrelevant. In the puzzle given, the non blues could be 1, 10, 1000,...
( Oh that was already stated )
What one has to consider is YOU as an islander, who does not know his eye color, and the deductive process to go through while perceiving only the blue-eyed and determining if your color is blue or non-blue

Yeah, I went through it. The point is that there are various "depths" of statements. Letting the blue-eyed islanders be numbered 1, 2, 3, etc.

1. There are actually 100 blue-eyed individuals.
2. Islander #1 believes that there are either 99 or 100 blue-eyed individuals.
3. Islander #1 believes that islander #2 believes that there are 98, 99 or 100 individuals
4. Islander #1 believes that islander #2 believes that islander #3 believes that there are 97, 98, 99 or 100 individuals.

So the reasoning involves considering "possible worlds" in which there are between 0 and 100 blue-eyed individuals. But in every possible world, there are 100 individuals doing the reasoning, although they aren't all blue-eyed in all possible worlds. So the non-blue-eyed people are relevant in other possible worlds.

 

[Heinera]

No. But he could make it happen one step earlier by saying that he sees at least 2 blue-eyed monks. The statement "there is at least one blue-eyed monk" is a very specific trigger to a very specific sequence.

That is not correct (the "No"). If the guru says that "everybody knows there is at least one blue-eyed monk", a group of two monks would immediately (and independently) deduce they both had blue eyes, and could thus skip a time step. (Monk A reasons that if he had brown eyes, monk B couldn't know there was at least one blue-eyed monk, and same for B vs. A). The induction that takes us to n > 2 goes as before.

Furthermore, if the guru says "everybody knows that everybody knows there is at least one blue-eyed monk" (to a group of size n >= 3) he would move the suicide moment forward by two time steps, etc. This clearly shows that the nested levels of knowledge are relevant to the problem.

 

[Demystifier]

For a last couple of days, I have not been answering any questions addressed to me. I wanted to think about carefully about all this ones again. In the next post I will present my last conclusions, which, I hope, answer many questions and objections addressed to me. If not, please refer any new questions/objections to my next post, which is supposed to surpass all my previous posts.

 

[Demystifier]

Refined critique of the standard solution

I have found a simpler and sharper way to explain what exactly is wrong with the standard solution. In my explanation I will assume that the reader is already familiar with the standard solution, which will allow me to skip over some details.

First let me present some crucial correct results of the standard solution:

(1) The information given by the prophet is sufficient for all blue-eyers to eventually realize that they are blue-eyers.

(2) If there are n blue-eyers, they will realize that they are blue-eyers after n days, starting from the first day at which they acquire information equivalent to the information given by the prophet.

In addition, if one assumes

(3) No other source of information, except by the prophet himself, provides sufficient information for all blue-eyers to eventually realize that they are blue-eyers.

then one arrives at the final result

(4) If there are n blue-eyers, they will realize that they are blue-eyers after n days, starting from the first day at which the information was given by the prophet.

Note that (1) and (2) are not sufficient to get (4). To get (4), one also needs (3). In other words, (3) is tacitly assumed in the standard solution that leads to the final result (4).

But assumption (3) is wrong. Consequently, the standard solution is wrong as well.

Why is (3) wrong? Well, (3) is correct for n=1 and n=2. But (3) is wrong when n=3 or more. Let me only explain why is (3) wrong for n=3, because the generalization for higher n is trivial.

The prophet made the public statement:
"Some of you has blue eyes."
Clearly, this is equivalent to the public statement:
"At least one of you has blue eyes."

But now consider the following scenario. Instead of making a public statement, to each monk the prophet gives a separate private envelope with a letter. Each letter contains the same message reading as follows:
"At least one of monks has blue eyes. This message is sent to all monks."
Clearly, this scenario provides information equivalent to the public statement above. Even though the letter is not public, the second sentence in the letter makes the same effect as publicity of the one-sentence public statement above.

Next observe that the two-sentence message above is equivalent to:
"At least one of monks has blue eyes. Now all monks know that."

Now the crucial question is this. Is the information provided by the prophet new to the monks? Let us study case by case.

n=1: For this single blue-eyer, the first sentence in the letter "At least one of monks has blue eyes" is new.

n=2: In this case, the blue-eyers already know that "At least one of monks has blue eyes". They know it without the prophet. It is not new. But the second sentence "Now all monks know that" is something new.

n=3: In this case the first sentence is not new, similarly to the case n=2. In addition, for n=3, even the second sentence is not new. (For instance, the first blue-eyer knows two blue-eyers (the second and the third one), he also knows that the second blue-eyer knows at least one blue-eyer (the third one), and finally he knows that the third blue-eyer also knows at least one blue-eyer (the second one).) Therefore nothing in the prophet's message is new in the case n=3. In other words, assumption (3) is wrong for n=3. Q.E.D.

 

[maline]

But now consider the following scenario. Instead of making a public statement, to each monk the prophet gives a separate private envelope with a letter. Each letter contains the same message reading as follows:
"At least one of monks has blue eyes. This message is sent to all monks."
Clearly, this scenario provides information equivalent to the public statement above. Even though the letter is not public, the second sentence in the letter makes the same effect as publicity of the one-sentence public statement above.

Next observe that the two-sentence message above is equivalent to:
"At least one of monks has blue eyes. Now all monks know that."

No, the statement "This message is sent to all monks" includes the second sentence as well: Everyone knows that everyone knows that everyone knows etc. that at least one of monks has blue eyes. This is nontrivially stronger than "Everyone knows that at least one of monks has blue eyes".

See andrewkirk's post # 94, I think it is the clearest thus far.

Also note that before the prophet speaks, no one has reacted in any way to anyone's eye color, so it is clear that no one can deduce his eye color from anyone else's actions. After the prophet speaks, you have agreed that the deduction can be made. There remains to clarify how this change comes about, which several posters including andrewkirk have done.

 

[Heinera]

n=3: In this case the first sentence is not new, similarly to the case n=2. In addition, for n=3, even the second sentence is not new. (For instance, the first blue-eyer knows two blue-eyers (the second and the third one), he also knows that the second blue-eyer knows at least one blue-eyer (the third one), and finally he knows that the third blue-eyer also knows at least one blue-eyer (the second one).) Therefore nothing in the prophet's message is new in the case n=3. In other words, assumption (3) is wrong for n=3. Q.E.D.

Before I can adress this, I need to know what you think will happen in the case n=3. If the monks are told about the suicide rule at t=0, will they commit suicide at t=3 even without any statement from the prophet?

 

[stevendaryl]

Next observe that the two-sentence message above is equivalent to:
"At least one of monks has blue eyes. Now all monks know that."

Not quite. The public announcement is equivalent to arbitrarily (as many levels as there are monks) nested statements:

1. At least one monk has blue eyes.
2. Now all monks know that.
3. Now all monks know that all monks know that.
4. Now all monks know that all monks know that all monks know that.
5. etc.

A public announcement accomplishes this, as does your self-referential private announcement ("At least one monk has blue eyes, and this message will be sent to each monk"), but your pair of sentences doesn't accomplish that.

Now the crucial question is this. Is the information provided by the prophet new to the monks? Let us study case by case.

n=1: For this single blue-eyer, the first sentence in the letter "At least one of monks has blue eyes" is new.

n=2: In this case, the blue-eyers already know that "At least one of monks has blue eyes". They know it without the prophet. It is not new. But the second sentence "Now all monks know that" is something new.

n=3: In this case the first sentence is not new, similarly to the case n=2. In addition, for n=3, even the second sentence is not new.

That's true, but your two sentences are not equivalent to the original announcement. Let's call our three islanders "Alice", "Bob", and "Carol". Assume that all three have blue eyes. Before any announcement, the situation is this:

1. Alice has blue eyes.
   
2. Alice knows that at least Bob and Carol have blue eyes.
3. Alice knows that Bob knows that at least Carol has blue eyes.
4. Similarly for other permutations of the names

What Alice doesn't know is whether Bob knows that Carol knows that there is at least one person with blue eyes.

The possible eye-situations before the announcement are described by the following "possible worlds":

1. World 1: Alice, Bob and Carol all have blue eyes.
2. World 2: Bob and Carol have blue eyes, but Alice doesn't.
3. World 3: Only Carol has blue eyes.
4. World 4: Nobody has blue eyes.

• In world 1, Alice believes that the actual world is either world 1 or world 2.
• In world 2, Bob believes that the actual world is either world 2 or world 3.
• In world 3, Carol believes that the actual world is either world 3 or world 4.

1. Alice believes it's possible that the actual world is world 2.
2. Alice believes it's possible that Bob thinks it's possible that the actual world is world 3.
3. Alice believes it's possible that Bob thinks it's possible that Carol thinks it's possible that the actual world is world 4.

After the public announcement that there is at least one blue-eyed individual, the first two sentences are unchanged, but the third sentence becomes:

Alice believes it's possible that Bob knows that Carol knows that the actual world is world 3. (Because world 4 has been ruled out by the announcement).

 

[.Scott]

That is not correct (the "No"). If the guru says that "everybody knows there is at least one blue-eyed monk", a group of two monks would immediately (and independently) deduce they both had blue eyes, and could thus skip a time step. (Monk A reasons that if he had brown eyes, monk B couldn't know there was at least one blue-eyed monk, and same for B vs. A). The induction that takes us to n > 2 goes as before.

Furthermore, if the guru says "everybody knows that everybody knows there is at least one blue-eyed monk" (to a group of size n >= 3) he would move the suicide moment forward by two time steps, etc. This clearly shows that the nested levels of knowledge are relevant to the problem.

You're right. Those statements are functionally equivalent to "there's at least 2 blue-eyed" and "there's at least 3 blue-eyed".

 

[stevendaryl]

Using graphs, the situation can be described as follows:

The actual world is W1, where all three have blue eyes. The arrows labeled "Alice" indicate which worlds Alice thinks are possible. She thinks W2 is possible. In world W2, only Carol and Bob have blue eyes. The arrows labeled "Bob" indicate which worlds Bob would think were possible, if the actual world were W2. So if the actual world were W2, then Bob would think that W3 is possible. In world W3, only Carol has blue eyes. If the actual world were W3, then Carol would think that W4 is possible. In world W4, nobody has blue eyes. So before the announcement, it's possible (according to Alice's information) that the actual world is W2, but Bob thinks that he's in W3, and Bob thinks that Carol thinks that she's in W4.

After the announcement, the situation is changed to the following:

After the announcement, Carol knows that the actual world is not W4. So Alice thinks it's possible that we're in world W2, but that Bob believes we're in world W3. In world W3, Carol knows that she has blue eyes (since she knows that she isn't in world W4). So in W3, Carol commits suicide. If Carol doesn't commit suicide, then Bob figures out that the actual world is not W3. So now the situation is:

Alice thinks it's possible that we're in world W2. But in world W2, Bob would know that he's in world W2 (since W3 has been eliminated as a possibility). So in W2, Bob would know that he's in world W2, and commit suicide.

If that doesn't happen, Alice knows that we're in world W1.

 

[Demystifier]

Before I can adress this, I need to know what you think will happen in the case n=3. If the monks are told about the suicide rule at t=0, will they commit suicide at t=3 even without any statement from the prophet?

Yes they will.

 

[stevendaryl]

Yes they will.

Once again, suppose the islanders are Alice, Bob and Carol. They all have blue eyes, but Alice erroneously believes that she has brown eyes. How would she ever come to know that she was mistaken?

 

[Demystifier]

@maline and @stevendaryl from your responses I can conclude that the main controversy is whether or not the message
"At least one of monks has blue eyes. This message is sent to all monks."
is equivalent to
"At least one of monks has blue eyes. Now all monks know that."

I say it's equivalent, and you say it's not. You say that the first message contains more relevant information than the second one. But intuitively, it doesn't make sense to me. So I need to think more about it.

 

[lukesfn]

With the above graph, have you thought about worlds where no announcements where made? That question always confuses me, sometimes I think they can be safely ignored, but sometimes I think that has been assumed without a fool proof justification.

I was also considering similar thoughts to what demystifier put quite clearly in post 139.

I've been reading numerous standard solutions, and they often describe them selves as an inductive solution, but I keep getting confused when I try to pin point the exact points where inductive reasoning is needed, rather then deductive.

I am wondering that if for that for certain numbers of blue eyed people, the inductive reasoning feels so strong that it is mistaken for deductive reasoning.

 

[Demystifier]

Once again, suppose the islanders are Alice, Bob and Carol. They all have blue eyes, but Alice erroneously believes that she has brown eyes. How would she ever come to know that she was mistaken?

But we are talking about logical people. There is no any logical reason for Alice to believe that she has brown eyes.

 

[Demystifier]

With the above graph, have you thought about worlds where no announcements where made?

Yes. My answer is that, for $n\geq 3$, they will all kill themselves after $n$ days, counting from the day at which they all together learned about the suicide law. This assumes that they did learn the suicide law together at the same day. If they learned it in another way, then the answer depends on how exactly did they learn it.